Question

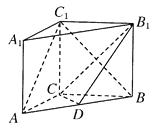
【题目】如图，在三棱锥中，平面平面， 为等边三角形， 且， 分别为的中点.

（1）求证： 平面.

（2）求证：平面平面.

（3）求三棱锥的体积.

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）.

【解析】试题分析：（1）分别是的中点，所以，所以平面.（2），又因为平面平面，所以平面，所以平面平面.（3）三棱锥的体积与三棱锥的体积相等，则利用等体积转化，得体积为.

试题解析：

（1）因为分别是的中点，

所以，

因为面， 平面，

所以平面.

（2）， 是的中点，

所以，

又因为平面平面，且平面，

所以平面，所以平面平面.

（3）在等腰直角三角形中， ，

所以， ，

所以等边三角形的面积，

又因为平面，

所以三棱锥的体积等于.

又因为三棱锥的体积与三棱锥的体积相等.