题目内容
已知函数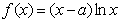 ,
,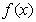 的导函数为
的导函数为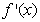 .
.
(Ⅰ)当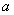 =0时,求
=0时,求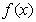 的最小值;
的最小值;
(Ⅱ)设 ,求函数
,求函数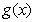 的单调区间.
的单调区间.
解:(Ⅰ)函数f(x)的定义域为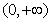 .
.
当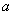 =0时,
=0时,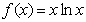 ,
, .
.
令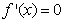 得
得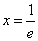 .
.
|
|
|
|
|
|
| - | 0 | + |
|
| 递减 | 极小值 | 递增 |
.
∴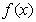 的最小值为
的最小值为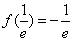 .
.
(Ⅱ)
∵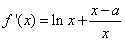
∴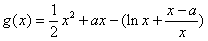 .
.
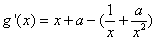 ,-
,-
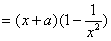 ,
,
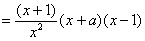 .
.
(1)当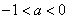 时,在
时,在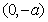 ,
,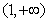 内
内 ;在
;在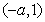 内
内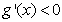 .
.
∴ 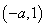 为递减区间,
为递减区间,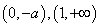 递增区间.
递增区间.
(2)当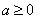 时,在
时,在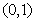 内,
内,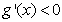 ;在
;在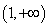 内,
内,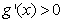 .
.
∴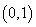 递减区间,
递减区间,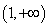 递增区间.
递增区间.
综上所述,当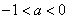 时,
时,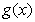 单调递增区间为
单调递增区间为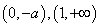 ,递减区
,递减区
间为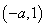 ;当
;当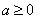 时,
时,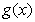 单调递增区间为
单调递增区间为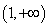 ,减区间为
,减区间为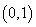 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
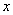
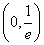
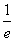
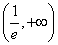
 :
: ,
, 的一边
的一边 为圆
为圆 长度的最大值是 .
长度的最大值是 .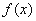 为奇函数,当
为奇函数,当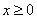 时,
时,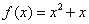 ,则
,则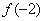 的值为 .
的值为 .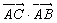 等于
等于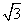 (C)2 (D)
(C)2 (D)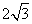
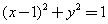 的圆心且与直线
的圆心且与直线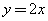 平行的直线方程是
平行的直线方程是 (B)
(B)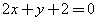 (C)
(C)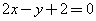 (D)
(D)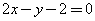
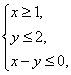 则
则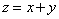 的最小值是___________.
的最小值是___________. 的双曲线的两条渐近线互相垂直,则此双曲线的实轴长为 ( )
的双曲线的两条渐近线互相垂直,则此双曲线的实轴长为 ( ) (B)
(B) 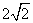 (D)
(D) 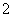
 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 ,
, ,
, ,则
,则 ______.
______.