题目内容
若α，β为锐角，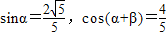
，则cosβ=（ ）A．
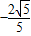
B．
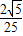
C．
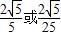
D．
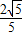
【答案】分析：由题意可求得cosα=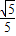
，sin（α+β）=
，再根据 cosβ=cos[（α+β）-α]，利用两角和差的余弦公式求得结果．
解答：解：若α，β为锐角，则0＜α+β＜π．再有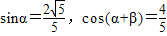
，
可得cosα=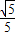
，sin（α+β）=
，
∴cosβ=cos[（α+β）-α]=cos（α+β）cosα+sin（α+β）sinα=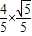
+
=
，
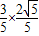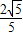故选D．
点评：本题主要考查同角三角函数的基本关系，两角和差的余弦公式的应用，属于中档题．
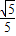，sin（α+β）=，再根据 cosβ=cos[（α+β）-α]，利用两角和差的余弦公式求得结果．解答：解：若α，β为锐角，则0＜α+β＜π．再有
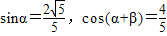，可得cosα=
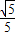，sin（α+β）=，∴cosβ=cos[（α+β）-α]=cos（α+β）cosα+sin（α+β）sinα=
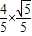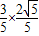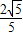+=，故选D．
点评：本题主要考查同角三角函数的基本关系，两角和差的余弦公式的应用，属于中档题．
练习册系列答案
开心练习课课练与单元检测系列答案
相关题目
已知点F1、F2分别是双曲线
-
=1的左、右焦点，过F1且垂直于x轴的直线与双曲线交于A、B两点，若△ABF2为锐角三角形，则该双曲线的离心率e的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、（1，+∞） | ||
B、(1，
| ||
| C、（1，2） | ||
D、(1，1+
|
已知函数f（x）的导函数图象如图所示，若△ABC为锐角三角形，则一定成立的是（ ）