题目内容
已知△ABC的三个内角A,B,C的对边分别为a,b,c,若a,b,c成等差数列,且2cos2B-8cosB+5=0,求角B的大小并判断△ABC的形状.
解法一:∵2cos2B-8cosB+5=0,?
∴2(2cos2B-1)-8cosB+5=0. ?
∴4cos2B-8cosB+3=0,即(2cosB-1)(2cosB-3)=0.??
解得cosB=![]() 或cosB=
或cosB=![]() (舍去),∴cosB=
(舍去),∴cosB=![]() . ?
. ?
∵0<B<π,∴B=![]() . ?
. ?
∵a,B,c成等差数列,∴a+c=2B. ?
∴cosB=![]() =
=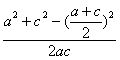 =
=![]() , ?
, ?
化简得a2+c2
∴△ABC是等边三角形. ?
解法二:∵2cos2B-8cosB+5=0,?
∴2(2cos2B-1)-8cosB+5=0. ?
∴4cos2B-8cosB+3=0,即(2cosB-1)(2cosB-3)=0.
解得cosB=![]() 或cosB=
或cosB=![]() (舍去),∴cosB=
(舍去),∴cosB=![]() . ?
. ?
∵0<B<π,∴B=![]() . ?
. ?
∵a,B,c成等差数列,∴a+c=2B. ?
由正弦定理得sinA+sinC=2sinB=2sin![]() =
=![]() , ?
, ?
∴sinA+sin(![]() -A)=
-A)=![]() .?
.?
∴sinA+sin![]() cosA-cos
cosA-cos![]() sinA=
sinA=![]() .?
.?
化简得![]() sinA+
sinA+![]() cosA=
cosA=![]() ,∴sin(A+
,∴sin(A+![]() )=1.?
)=1.?
∵0<A<π,∴A+![]() =
=![]() .?
.?
∴A=![]() ,C=
,C=![]() . ?
. ?
∴△ABC是等边三角形.
