题目内容
函数 在其定义域上是( )
在其定义域上是( )
| A.奇函数 | B.偶函数 | C.增函数 | D.减函数 |
B
解析试题分析:因为f(x)=2sin(x+ )=2cosx,那么可知在其定义域内有增区间也有减区间,并且呈现周期性出现,而f(-x)=2cos(-x)=2cosx=f(x),且定义域为R,因此利用偶函数的定义可知选B.
)=2cosx,那么可知在其定义域内有增区间也有减区间,并且呈现周期性出现,而f(-x)=2cos(-x)=2cosx=f(x),且定义域为R,因此利用偶函数的定义可知选B.
考点:本试题主要考查了函数的单调性和奇偶性的判定。
点评:解决该试题的关键是将函数式化到最简,然后结合定义判定。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设函数 的最小正周期为
的最小正周期为 ,且
,且 ,则( )
,则( )
A.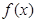 在 在 单调递减 单调递减 | B.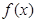 在 在 单调递减 单调递减 |
C.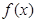 在 在 单调递增 单调递增 | D.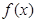 在 在 单调递增 单调递增 |
已知 ,则
,则 ( )
( )
A. | B. | C. | D. |
函数 的部分图象如图所示,则
的部分图象如图所示,则 的值等于 ( )
的值等于 ( )
A. | B. | C. | D. |
为了得到函数 的图像,只需把函数
的图像,只需把函数 的图像
的图像
A.向左平移 个长度单位 个长度单位 | B.向右平移 个长度单位 个长度单位 |
C.向左平移 个长度单位 个长度单位 | D.向右平移 个长度单位 个长度单位 |
函数 为奇函数,且在
为奇函数,且在 上为减函数的
上为减函数的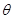 值可以是
值可以是
A. | B. | C. | D. |
若方程 的任意一组解(
的任意一组解( )都满足不等式
)都满足不等式 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
 是实数,则函数
是实数,则函数 的图象不可能是( )
的图象不可能是( )
 的图像上所有的点向右平行移动
的图像上所有的点向右平行移动 个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是( )
个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是( )


