题目内容
函数 为奇函数,且在
为奇函数,且在 上为减函数的
上为减函数的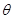 值可以是
值可以是
A. | B. | C. | D. |
D
解析试题分析:因为函数 为奇函数,而
为奇函数,而 ,那么则有f(-x)=-f(x),则有
,那么则有f(-x)=-f(x),则有 ,展开化简可知2sin2xcos
,展开化简可知2sin2xcos =0,
=0, ,故函数f(x)=
,故函数f(x)= ,又因为在
,又因为在 上为减函数,故可知令k=1,可知
上为减函数,故可知令k=1,可知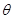 =
= ,代入得到f(x)=
,代入得到f(x)= ,结合正弦函数图像和性质可知满足题意故选D。
,结合正弦函数图像和性质可知满足题意故选D。
考点:本试题主要考查了三角函数的奇偶性和单调性的运用。
点评:解决该试题的关键是对于三角函数性质的研究先将函数化为单一三角函数,然后结合性质分析得到。

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
设角 的终边经过点
的终边经过点 ,那么
,那么
A. | B. | C. | D. |
函数 在其定义域上是( )
在其定义域上是( )
| A.奇函数 | B.偶函数 | C.增函数 | D.减函数 |
已知函数 ,则
,则 的值域是
的值域是
A. | B. | C. | D. |
函数 的最小正周期等于 ( )
的最小正周期等于 ( )
A. | B.2 | C. | D. |
已知等腰三角形顶角的余弦值等于 ,则这个三角形底角的正弦值为( )
,则这个三角形底角的正弦值为( )
A. | B. | C. | D. |
若 ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
已知 为第四象限的角,且
为第四象限的角,且
A. | B. | C. | D. |
已知 ,
, ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |