题目内容
已知 是实数,则函数
是实数,则函数 的图象不可能是( )
的图象不可能是( )
D
解析试题分析:函数f(x)=1+asinax的图象是一个正弦曲线型的图,其振幅为|a|,周期为 ,周期与振幅成反比,从这个方向观察四个图象。
,周期与振幅成反比,从这个方向观察四个图象。
对于振幅大于1时,三角函数的周期为:T= ,∵|a|>1,∴T<2π,而D不符合要求,它的振幅大于1,但周期反而大于了2π.
,∵|a|>1,∴T<2π,而D不符合要求,它的振幅大于1,但周期反而大于了2π.
对于选项A,a<1,T>2π,满足函数与图象的对应关系,
故选D.
考点:本试题主要考查了函数图像的正确表示。
点评:由于函数的解析式中只含有一个参数,这个参数影响振幅和周期,故振幅与周期相互制约,这是本题的关键

练习册系列答案
相关题目
若f(x)=tan ,则 ( )
,则 ( )
| A.f(0)>f(-1)>f(1) | B.f(0)>f(1)>f(-1) |
| C.f(1)>f(0)>f(-1) | D.f(-1)>f(0)>f(1) |
为了得到函数 的图象,只需把函数
的图象,只需把函数 的图象( )
的图象( )
A.向左平移 个长度单位 个长度单位 | B.向右平移 个长度单位 个长度单位 |
C.向左平移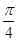 个长度单位 个长度单位 | D.向右平移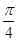 个长度单位 个长度单位 |
函数 在其定义域上是( )
在其定义域上是( )
| A.奇函数 | B.偶函数 | C.增函数 | D.减函数 |
 为第四象限角,
为第四象限角, ,则
,则 =
=
A. | B. | C. | D. |
已知函数 ,则
,则 的值域是
的值域是
A. | B. | C. | D. |
函数 的最小正周期等于 ( )
的最小正周期等于 ( )
A. | B.2 | C. | D. |
若 ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
已知 ,且
,且 为第二象限角,则
为第二象限角,则 ( )
( )
A. | B. | C. | D. |