题目内容
已知定义在区间 上的函数
上的函数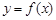 的图象关于直线
的图象关于直线 对称,当
对称,当 时,函数
时,函数 ,其图象如图所示.
,其图象如图所示.
(Ⅰ)求函数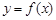 在
在 的表达式;
的表达式;
(Ⅱ)求方程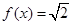 的解;
的解;
(Ⅲ)是否存在常数 的值,使得
的值,使得
 上恒成立;若存在,求出
上恒成立;若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(1)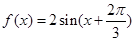
(2)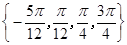
(3)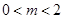
解析试题分析:解:(Ⅰ)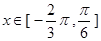 ,
,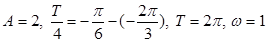 1分
1分
且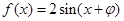 过
过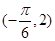 ,∵
,∵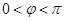
∴ 3分
3分
当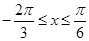 时,
时,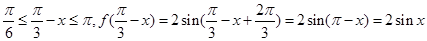
而函数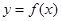 的图象关于直线
的图象关于直线 对称,则
对称,则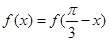
即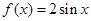 ,
,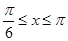 5分
5分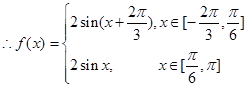 6分
6分
(Ⅱ)当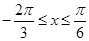 时,
时,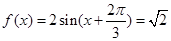
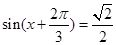
∴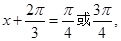 即
即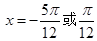 8分
8分
当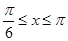 时,
时,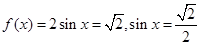
∴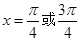
∴方程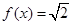 的解集是
的解集是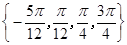 10分
10分
(Ⅲ)存在 假设存在,由条件得: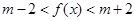 在
在 上恒成立
上恒成立
即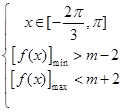 ,由图象可得:
,由图象可得: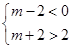
∴ 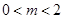 所以假设成立 14分
所以假设成立 14分
考点:三角函数的图像与性质的运用
点评:主要是考查了函数的图像与性质的运用,属于中档题。

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
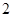 的等比数列
的等比数列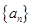 中,
中,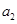 与
与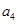 的等差中项是
的等差中项是 .
.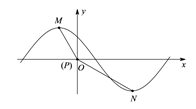
 的值;
的值;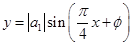 ,
,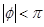 ,的一部分图像如图所示,
,的一部分图像如图所示, ,
, 为图像上的两点,设
为图像上的两点,设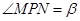 ,其中
,其中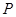 与坐标原点
与坐标原点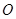 重合,
重合,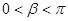 ,求
,求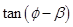 的值.
的值.

 的图像的一部分如图所示.
的图像的一部分如图所示.
 的解析式;
的解析式; 的最值;
的最值;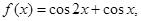
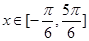 ,求函数
,求函数 的值域.
的值域. .
.
 在长度为一个周期的闭区间上的简图;
在长度为一个周期的闭区间上的简图; 的图象作怎样的变换可得到
的图象作怎样的变换可得到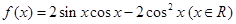 .
.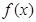 的最小正周期;
的最小正周期;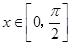 时,求函数
时,求函数 Rl,其中R为扇形半径,l为弧长)
Rl,其中R为扇形半径,l为弧长)
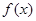 的最小正周期及单调递增区间;
的最小正周期及单调递增区间; 中,若
中,若 ,
, ,
, ,求
,求 的值.
的值.