题目内容
7.已知函数f(x)=x2-2lnx.(1)求证:f(x)在(1,+∞)上单调递增.
(2)若f(x)≥2tx-$\frac{1}{{x}^{2}}$在x∈(0,1]内恒成立,求实数t的取值范围.
分析 (1)先求函数的导数,根据导数和函数的单调性的关系即可求出,
(2)要求若f(x)≥2tx-$\frac{1}{{x}^{2}}$在x∈(0,1]内恒成立,即转化为2t≤x+$\frac{1}{{x}^{3}}$-$\frac{2lnx}{x}$在x∈(0,1]内恒成立,只需求h(x)=x+$\frac{1}{{x}^{3}}$-$\frac{2lnx}{x}$x∈(0,1]内的最小值即可.
解答 解:(1)证明:函数的定义域为(0,+∞),f′(x)=2x-$\frac{2}{x}$=$\frac{2(x+1)(x-1)}{x}$,
由f′(x)>0,得x>1,由f′(x)<0,得0<x<1,
所以,函数f(x)在区间(1,+∞)上单调递增.
(2)由f(x)≥2tx-$\frac{1}{{x}^{2}}$对x∈(0,1]恒成立,得2t≤x+$\frac{1}{{x}^{3}}$-$\frac{2lnx}{x}$.
令h(x)=x+$\frac{1}{{x}^{3}}$-$\frac{2lnx}{x}$,则h′(x)=$\frac{{x}^{4}-2{x}^{2}-3+2{x}^{2}lnx}{{x}^{4}}$,
因为x∈(0,1],所以x4-3<0,-2x2<0,
2x2lnx<0,x4>0,
所以h′(x)<0,
所以h(x)在(0,1)上为减函数.
所以当x=1时,h(x)=h(x)=x+$\frac{1}{{x}^{3}}$-$\frac{2lnx}{x}$,有最小值2,得2t≤2,
所以t≤1,故t的取值范围是(-∞,1].
点评 本题考查了利用导数求闭区间上函数的最值,以求函数恒成立问题,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.在极坐标系中,点M(2,$\frac{π}{3}$)到直线l:ρsin(θ+$\frac{π}{4}$)=$\frac{{\sqrt{2}}}{2}$的距离为( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{3}{2}$ | D. | $\sqrt{2}$ |
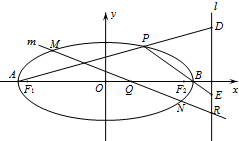 椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1,F2分别是它的左、右焦点,已知椭圆C过点(0,1),且离心率e=$\frac{2\sqrt{2}}{3}$.
椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1,F2分别是它的左、右焦点,已知椭圆C过点(0,1),且离心率e=$\frac{2\sqrt{2}}{3}$.