Question

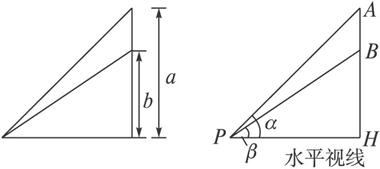
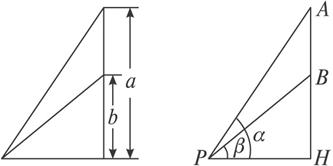
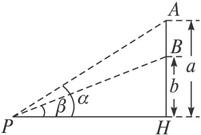
如图，教室的墙壁上挂着一块黑板，它的上、下边缘分别在学生的水平视线上方a m和b m，问学生距墙壁多远时看黑板的视角最大?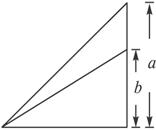

                         

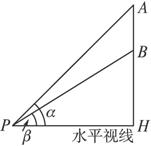
Answer 1

思路分析:设学生P距黑板x m，黑板上、下边缘与学生P的水平视线PH的夹角分别是∠APH=α,∠BPH=β,其中α＞β,则学生看黑板的视角为α-β,剩下的就是如何把α-β与变量x联系起来建立一个数学模型的问题了.

解:tanα=,tanβ=,由此可得tan(α-β)=.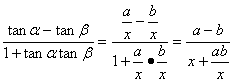

因为x+≥2,

当且仅当x=时，tan(α-β)最大.

又由于α-β为锐角，所以此时α-β也最大，

亦即学生距墙壁为(m)时看黑板的视角最大.