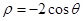题目内容
在极坐标系中,圆心为 ,且过极点的圆的方程是
,且过极点的圆的方程是
- A.ρ=2sinθ
- B.ρ=-2sinθ
- C.ρ=2cosθ
- D.ρ=-2cosθ
A
分析:先在直角坐标系下求出圆心在 ,且过极点的圆的直角坐标方程,再利用直角坐标与极坐标的互化公式化成极坐标方程即可.
,且过极点的圆的直角坐标方程,再利用直角坐标与极坐标的互化公式化成极坐标方程即可.
解答:∵在极坐标系中,圆心在 ,且过极点的圆的直角坐标方程是:
,且过极点的圆的直角坐标方程是:
x2+(y-1)2=1,即x2+y2-2y=0,
它的极坐标方程为:ρ=2sinθ.
故选A.
点评:本题考查简单曲线的极坐标方程、点的极坐标和直角坐标的互化,能在极坐标系中用极坐标刻画圆的位置.
分析:先在直角坐标系下求出圆心在
 ,且过极点的圆的直角坐标方程,再利用直角坐标与极坐标的互化公式化成极坐标方程即可.
,且过极点的圆的直角坐标方程,再利用直角坐标与极坐标的互化公式化成极坐标方程即可.解答:∵在极坐标系中,圆心在
 ,且过极点的圆的直角坐标方程是:
,且过极点的圆的直角坐标方程是:x2+(y-1)2=1,即x2+y2-2y=0,
它的极坐标方程为:ρ=2sinθ.
故选A.
点评:本题考查简单曲线的极坐标方程、点的极坐标和直角坐标的互化,能在极坐标系中用极坐标刻画圆的位置.

练习册系列答案
相关题目
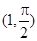 ,且过极点的圆的方程是 (
)
,且过极点的圆的方程是 (
)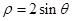 (B)
(B)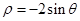 (C)
(C)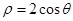 ( D)
( D)