题目内容
在正四棱柱ABCD-A1B1C1D1中，点P是底面ABCD的对角线AC上的动点，则下列说法正确的是（ ）
分析：直接根据正四棱柱ABCD-A1B1C1D1中，有BD⊥AC，BD⊥AA1；得到BD⊥平面ACC1A1；进而得到平面BDC1⊥平面ACC1A1；再结合平面A1PC1与平面ACC1A1重合即可得到答案A成立．B，C，D均可举出反例说明其不成立．
解答：解：
因为在正四棱柱ABCD-A1B1C1D1中，
有BD⊥AC，BD⊥AA1；
且AC∩AA1=A；
∴BD⊥平面ACC1A1；
BD⊆平面BDC1；
∴平面BDC1⊥平面ACC1A1；
∵点P是底面ABCD的对角线AC上的动点；
∴平面A1PC1与平面ACC1A1重合．
故平面BC1D与平面A1PC1一定垂直．
故选：A．
因为在正四棱柱ABCD-A1B1C1D1中，
有BD⊥AC，BD⊥AA1；
且AC∩AA1=A；
∴BD⊥平面ACC1A1；
BD⊆平面BDC1；
∴平面BDC1⊥平面ACC1A1；
∵点P是底面ABCD的对角线AC上的动点；
∴平面A1PC1与平面ACC1A1重合．
故平面BC1D与平面A1PC1一定垂直．
故选：A．
点评：本题主要考查平面之间的位置关系．一般在证明面面垂直时，常用面面垂直的判定定理：如果一个平面经过另一个平面的垂线，那么这两个平面互相垂直．
练习册系列答案
相关题目
如图，在正四棱柱ABCD-A1B1C1D1中，棱长AA1=2，AB=1，E是AA1的中点．
在正四棱柱ABCD-A1B1C1D1中，AA1=2AB，E为CC1的中点．
如图，在正四棱柱ABCD-A1B1C1D1中，AB=1，AA1=2，M、N分别为B1B和A1D的中点．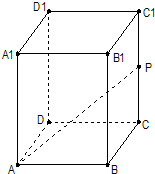
（2012•长宁区一模）在正四棱柱ABCD-A1B1C1D1中，已知底面ABCD的边长为2，点P是CC1的中点，直线AP与平面BCC1B1成30°角，求异面直线BC1和AP所成角的大小．（结果用反三角函数值表示）
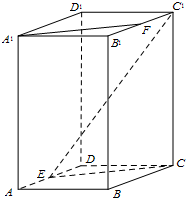（2012•昌平区二模）在正四棱柱ABCD-A1B1C1D1中，E为AD中点，F为B1C1中点．