题目内容

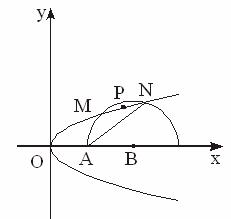
已知抛物线y2=4ax(a＞0)的焦点为A，以B(a+4,0)为圆心，|AB|长为半径，在x轴上方的半圆交抛物线于不同的两点M、N,P是MN的中点.

(1)求|AM|+|AN|的值;

(2)是否存在这样的a值,使|AM|、|AP|、|AN|成等差数列?

 

解:如图,A(a,0),∵|AB|=4,∴圆的方程为［x－(a+4)］2+y2=16,与y2=4ax联立得x2+2(a－4)x+8a+a2=0.

∴Δ=4(a－4)2－4(a2+8a)＞0.

解得0＜a＜1.

x1+x2=－2(a－4),x1·x2=a2+8a.

设M(x1,y1),N(x2,y2),

则|AM|=x1+a,|AN|=x2+a,

∴|AM|+|AN|=x1+x2+2a=－2a+8+2a=8.

(2)设P(x0,y0),则2x0=x1+x2,2y0=y1+y2.

∴2y0=2(+).

∴y0=+=··.

∴P(4－a,·.

若|AM|、|AP|、|AN|成等差数列,则|AP|=4.

∴(4－2a)2+a(8－2a+2)=16.

解得a=1.这与0＜a＜1矛盾.

故不存在a,使|AM|、|AP|、|AN|成等差数列.

点评:两条曲线交点的个数与由两曲线的方程所组成的方程组的个数是一一对应的.


练习册系列答案
相关题目
已知抛物线C1：y2=4ax（a＞0），椭圆C以原点为中心，以抛物线C1的焦点为右焦点，且长轴与短轴之比为
2
，过抛物线C1的焦点F作倾斜角为
π
4
的直线l，交椭圆C于一点P（点P在x轴上方），交抛物线C1于一点Q（点Q在x轴下方）．
（1）求点P和Q的坐标；
（2）将点Q沿直线l向上移动到点Q′，使|QQ′|=4a，求过P和Q′且中心在原点，对称轴是坐标轴的双曲线的方程．
（2003•东城区二模）已知抛物线C1：y2=4ax（a＞0），椭圆C以原点为中心，以抛物线C1的焦点为右焦点，且长轴与短轴之比为
2
，过抛物线C1的焦点F作倾斜角为
π
4
的直线l，交椭圆C于一点P（点P在x轴上方），交抛物线C1于一点Q（点Q在x轴下方）．
（Ⅰ）求点P和Q的坐标；
（Ⅱ）将点Q沿直线l向上移动到点Q′，使|QQ′|=4a，求过P和Q′且中心在原点，对称轴是坐标轴的双曲线的方程；
（Ⅲ）设点A（t，0）（常数t＞4），当a在闭区间〔1，2〕内变化时，求△APQ面积的最大值，并求相应a的值．
已知抛物线y2=4a（x+a）（a＞0），过原点O作一直线交抛物线于A、B两点，如图所示，试求|OA|·|OB|的最小值。
已知抛物线C1：y2=4ax（a＞0），椭圆C以原点为中心，以抛物线C1的焦点为右焦点，且长轴与短轴之比为
2
，过抛物线C1的焦点F作倾斜角为
π
4
的直线l，交椭圆C于一点P（点P在x轴上方），交抛物线C1于一点Q（点Q在x轴下方）．
（1）求点P和Q的坐标；
（2）将点Q沿直线l向上移动到点Q′，使|QQ′|=4a，求过P和Q′且中心在原点，对称轴是坐标轴的双曲线的方程．
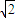已知抛物线C1：y2=4ax（a＞0），椭圆C以原点为中心，以抛物线C1的焦点为右焦点，且长轴与短轴之比为，过抛物线C1的焦点F作倾斜角为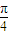的直线l，交椭圆C于一点P（点P在x轴上方），交抛物线C1于一点Q（点Q在x轴下方）．
（1）求点P和Q的坐标；
（2）将点Q沿直线l向上移动到点Q′，使|QQ′|=4a，求过P和Q′且中心在原点，对称轴是坐标轴的双曲线的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网