题目内容
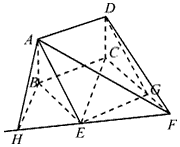
如图,矩形ABCD和梯形BEFC所在平面互相垂直,∠BCF=∠CEF=90°,AD=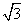 ,EF=2,
,EF=2,
(1)求证:AE∥平面DCF;
(2)求证:EF⊥平面DCE;
(3)当AB的长为何值时,二面角A-EF-C的大小为60°?
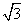 ,EF=2,
,EF=2, (1)求证:AE∥平面DCF;
(2)求证:EF⊥平面DCE;
(3)当AB的长为何值时,二面角A-EF-C的大小为60°?
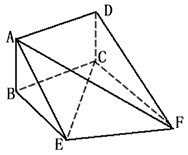
| (1)证明:过点E作EG⊥CF交CF于G,连结DG, 可得四边形BCGE为矩形, 又ABCD为矩形,所以AD⊥∥EG, 从而四边形ADGE为平行四边形, 故AE∥DG。 因为AE 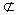 平面DCF,DG 平面DCF,DG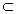 平面DCF, 平面DCF,所以AE∥平面DCF。 (2)证明:由平面ABCD⊥平面BEFG,DC⊥BC, 得DC⊥平面BEFC, 所以DC⊥EF, 又EF⊥EC,DC与EC交于点C, 所以EF⊥平面DCE。 (3)解:过点B作BH⊥EF交FE的延长线于H,连结AH, 由平面ABCD⊥平面BEFG,AB⊥BC, 得AB⊥平面BEFC, 从而AH⊥EF, 所以∠AHB为二面角A-EF-C的平面角, 在Rt△EFG中,因为EG=AD= 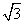 ,EF=2, ,EF=2,所以 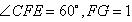 , , 又因为CE⊥EF,所以CF=4, 从而BE=CG=3,于是BH=BE·sin∠BEH= 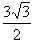 , , 因为AB=BH·tan∠AHB, 所以当AB为 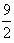 时,二面角A-EF-G的大小为60°。 时,二面角A-EF-G的大小为60°。 |
 |

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
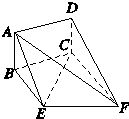 如图,矩形ABCD和梯形BEFC所在平面互相垂直,∠BCF=∠CEF=90°,AD=
如图,矩形ABCD和梯形BEFC所在平面互相垂直,∠BCF=∠CEF=90°,AD= 如图,矩形ABCD和梯形BEFC所在的平面互相垂直,BE∥CF,BE<CF,∠BCF=
如图,矩形ABCD和梯形BEFC所在的平面互相垂直,BE∥CF,BE<CF,∠BCF= 如图,矩形ABCD和矩形BCEF所在平面互相垂直,G为边BF上一点,∠CGE=90°,
如图,矩形ABCD和矩形BCEF所在平面互相垂直,G为边BF上一点,∠CGE=90°, 如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD=
如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD= 如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD=
如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD=