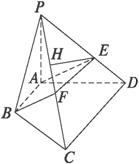
题目内容
如图已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,PD⊥底面ABCD,E、F分别为棱BC、AD的中点。
(Ⅰ)若PD=1,求异面直线PB和DE所成角的余弦值;
(Ⅱ)若二面角P-BF-C的余弦值为 ,求四棱锥P-ABCD 的体积。
,求四棱锥P-ABCD 的体积。
(Ⅰ)若PD=1,求异面直线PB和DE所成角的余弦值;
(Ⅱ)若二面角P-BF-C的余弦值为
 ,求四棱锥P-ABCD 的体积。
,求四棱锥P-ABCD 的体积。
解:(Ⅰ)E,F分别为棱BC,AD的中点,ABCD是边长为2的正方形 且 且 为平行四边形, 为平行四边形, 是PB与DE的所成角, 是PB与DE的所成角, 中,BF= 中,BF= ,PF= ,PF= ,PB=3 ,PB=3 , , 异面直线PB和DE所成角的余弦为 异面直线PB和DE所成角的余弦为 ; ;(Ⅱ)以D为原点,射线DA,DC,DP分别为x,y,z轴建立空间直角坐标系.设PD=a, 可得如下点的坐标: P(0,0,a),F(1,0,0),B(2,2,0),则有:  , ,因为PD⊥底面ABCD,所以平面ABCD的一个法向量为  , , 设平面PFB的一个法向量为  , ,则可得  即  令x=1,得  , ,所以  , ,由已知,二面角P-BF-C的余弦值为  , ,所以得:  , , 解得  , ,因为PD是四棱锥P-ABCD的高,所以,其体积为  。 。 |
 |

练习册系列答案
相关题目
 如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.
如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1. 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知 如图,已知四棱锥P-ABCD的底面ABCD是平行四边形,PA=AB=AD=a,
如图,已知四棱锥P-ABCD的底面ABCD是平行四边形,PA=AB=AD=a,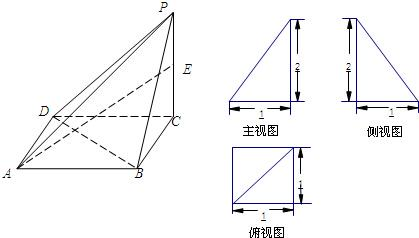 (2010•广东模拟)已知四棱锥P-ABCD的三视图如图所示,其中主视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.E是侧棱PC上的动点.
(2010•广东模拟)已知四棱锥P-ABCD的三视图如图所示,其中主视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.E是侧棱PC上的动点.