��Ŀ����
 ��A��Բx2+y2=1�ϵĶ��㣬��A��x���ϵ�ͶӰΪB����P��AB�ϣ��ǵ�P�Ĺ켣Ϊ����C����ԭ��б��Ϊk��ֱ�߽�����C��M��N���㣨����M�ڵ�һ���ޣ���MG��x���ڵ�G������NG��ֱ��NG������C����һ��H��
��A��Բx2+y2=1�ϵĶ��㣬��A��x���ϵ�ͶӰΪB����P��AB�ϣ��ǵ�P�Ĺ켣Ϊ����C����ԭ��б��Ϊk��ֱ�߽�����C��M��N���㣨����M�ڵ�һ���ޣ���MG��x���ڵ�G������NG��ֱ��NG������C����һ��H��������PΪAB���е㣬������C�ı����̣�
��������P����|AB|=m|PB|��m��0��m��1����������C�ķ��̣���̽���Ƿ����ʵ��m��ʹ�ö�����k��0������MN��MH�������ڣ����m��ֵ���������ڣ���˵�����ɣ�
���㣺ֱ����Բ���ߵ��ۺ�����
ר�⣺Բ�����е���ֵ�뷶Χ����
������������P��x��y������A��x��2y������x2+y2=1���������C�ı����̣�
������P��x��y������A��x��my��������x2+y2=1������C�ķ���Ϊx2+m2y2=1���ɴ����õ����������ʵ��m=
��ʹ�ö�����k��0������MN��MH��
������P��x��y������A��x��my��������x2+y2=1������C�ķ���Ϊx2+m2y2=1���ɴ����õ����������ʵ��m=
| 2 |
���
�⣺������P��x��y������A��x��2y��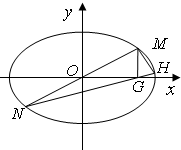
����x2+y2=1��x2+4y2=1��
������C�ı�����Ϊx2+
=1����4�֣�
������P��x��y������A��x��my��������x2+y2=1��
����C�ķ���Ϊx2+m2y2=1����6�֣�
��������M��x0��y0����H��x1��y1����
��N��-x0��-y0����G��x0��0����
��N��G��H���㹲�ߣ���kNH=kNG��
��
=
��kMN=
=
����7�֣�
��M��H������C�ϣ�
��x02+m2y02=1��x12+m2y12=1��
��ʽ����ã�kMH=
=-
����8�֣�
��kMH•kNM=-
•
=-
•
=-
����10�֣�
��MN��MH����kMH•kNM=-1����-
=-1��
��m��0��m��1����m=
��
�����ʵ��m=
��ʹ�ö�����k��0������MN��MH�� ����12�֣�

����x2+y2=1��x2+4y2=1��
������C�ı�����Ϊx2+
| y2 | ||
|
������P��x��y������A��x��my��������x2+y2=1��
����C�ķ���Ϊx2+m2y2=1����6�֣�
��������M��x0��y0����H��x1��y1����
��N��-x0��-y0����G��x0��0����
��N��G��H���㹲�ߣ���kNH=kNG��
��
| y0 |
| 2x0 |
| y1+y0 |
| x1+x0 |
| y0 |
| x0 |
| 2(y1+y0) |
| x1+x0 |
��M��H������C�ϣ�
��x02+m2y02=1��x12+m2y12=1��
��ʽ����ã�kMH=
| y1-y0 |
| x1-x0 |
| x0+x1 |
| m2(y0+y1) |
��kMH•kNM=-
| x0+x1 |
| m2(y0+y1) |
| y0 |
| x0 |
| x0+x1 |
| m2(y0+y1) |
| 2(y1+y0) |
| x1+x0 |
| 2 |
| m2 |
��MN��MH����kMH•kNM=-1����-
| 2 |
| m2 |
��m��0��m��1����m=
| 2 |
�����ʵ��m=
| 2 |
���������⿼�������뷽�̡���Բ��Բ�ķ��̼��ļ������ʡ�ֱ����Բ���ߵ�λ�ù�ϵ�Ȼ���֪ʶ�������������ͷ���̽�������������������ν��˼�롢������ת��˼�룮

��ϰ��ϵ�д�
 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�
�����Ŀ
����ż�����±��ų�4�У�

��2000�ڣ�������

��2000�ڣ�������
| A����125����1�� |
| B����125����2�� |
| C����250����1�� |
| D����250����4�� |
 ��֪����f��x��=Asin����x+ϕ����A��0���أ�0��0��ϕ���У���ͼ����ͼ��ʾ��
��֪����f��x��=Asin����x+ϕ����A��0���أ�0��0��ϕ���У���ͼ����ͼ��ʾ��