题目内容
本小题满分14分)如图,四棱锥E—ABCD中,ABCD是矩形,平面EAB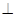 平面ABCD,AE=EB=BC=2,F为CE上的点,
平面ABCD,AE=EB=BC=2,F为CE上的点,
且BF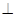 平面ACE.
平面ACE.
(1)求证:AE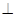 BE;
BE;
(2)求三棱锥D—AEC的体积;
(3)求二面角A—CD—E的余弦值.
【答案】
解:(1) ABCD是矩形,
ABCD是矩形,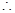 BC
BC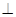 AB,
AB, 平面EAB
平面EAB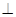 平面ABCD,
平面ABCD,
平面EAB 平面ABCD=AB,BC
平面ABCD=AB,BC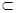 平面ABCD,
平面ABCD,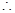 BC
BC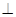 平面EAB,
平面EAB,
 EA
EA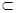 平面EAB,
平面EAB,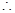 BC
BC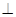 EA ,
EA , BF
BF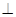 平面ACE,EA
平面ACE,EA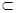 平面ACE,
平面ACE,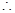 BF
BF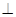 EA,
EA, BC
BC
 BF=B,BC
BF=B,BC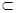 平面EBC,BF
平面EBC,BF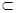 平面EBC,
平面EBC,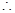 EA
EA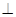 平面EBC ,
平面EBC , BE
BE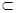 平面EBC,
平面EBC,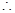 EA
EA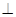 BE。
BE。
(2) EA
EA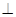 BE,
BE,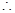 AB=
AB=
 ,设O为AB的中点,连结EO,
,设O为AB的中点,连结EO,
 ∵AE=EB=2,
∵AE=EB=2,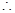 EO
EO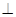 AB,
AB, 平面EAB
平面EAB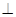 平面ABCD,
平面ABCD, EO
EO 平面ABCD,即EO为三棱锥E—ADC的高,且EO=
平面ABCD,即EO为三棱锥E—ADC的高,且EO= ,
,
 。
。
(3)以O为原点,分别以OE、OB所在直线为 ,如图建立空间直角坐标系,则
,如图建立空间直角坐标系,则 ,
,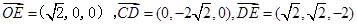 ,由(2)知
,由(2)知 是平面ACD的一个法向量,设平面ECD的法向量为
是平面ACD的一个法向量,设平面ECD的法向量为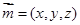 ,则
,则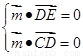 ,即
,即 ,令
,令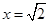 ,则
,则 ,所以
,所以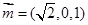 ,设二面角A—CD—E的平面角的大小为
,设二面角A—CD—E的平面角的大小为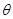 ,由图得
,由图得 ,
,
所以二面角A—CD—E的余弦值为 。
。
【解析】略

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
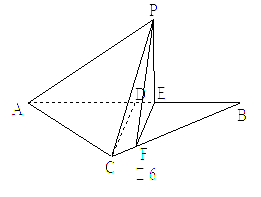 记BE=x,V(x)表示四棱锥P-ACFE的体积。
记BE=x,V(x)表示四棱锥P-ACFE的体积。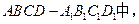
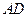
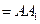
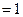
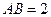
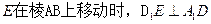 ;
;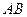 上是否存在点
上是否存在点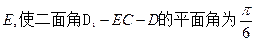 ?若存在,求出
?若存在,求出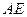 的长;若不存在,请说明理由.
的长;若不存在,请说明理由. 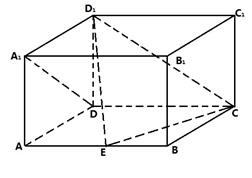
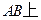
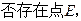 使
使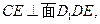 若存在,求出
若存在,求出 ,曲线段.DE上
,曲线段.DE上
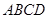 是边长为4的正方形,
是边长为4的正方形,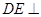 平面
平面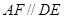 ,
,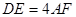 。
。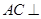 平面
平面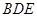 ;
;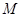 是线段
是线段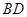 上一个动点,试确定点
上一个动点,试确定点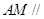 平面
平面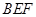 ,并
,并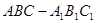 中,
中,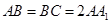 ,
,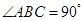 ,
,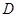 是
是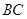 的中点.
的中点.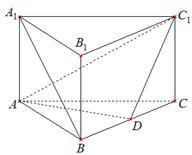
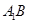 ∥平面
∥平面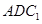 ;
;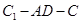 的余弦值;
的余弦值;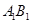 上是否存在点
上是否存在点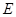 ,使
,使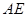 与
与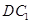 成
成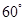 角?若存在,确定
角?若存在,确定