题目内容
已知两个不相等的平面向量 ,
, (
( )满足|
)满足| |=2,且
|=2,且 与
与 -
- 的夹角为120°,则|
的夹角为120°,则| |的最大值是
|的最大值是
 ,
, (
( )满足|
)满足| |=2,且
|=2,且 与
与 -
- 的夹角为120°,则|
的夹角为120°,则| |的最大值是
|的最大值是
试题分析:根据题意,由于两个不相等的平面向量
 ,
,  (
( )满足|
)满足| |=2,且
|=2,且 与
与 -
- 的夹角为120°,即可知
的夹角为120°,即可知 ,那么可知2
,那么可知2 =
= ,展开利用向量数量积的性质可知得到|
,展开利用向量数量积的性质可知得到| |的二次函数,利用二次函数性质可知其模的最大值为
|的二次函数,利用二次函数性质可知其模的最大值为 。故答案为
。故答案为 。
。点评:本题主要考查了向量的平行四边形法则的应用,三角形的正弦定理及正弦函数性质的简单应用

练习册系列答案
相关题目
 ,且
,且 ,则向量
,则向量 与
与 的夹角为( )
的夹角为( ) ,若
,若 和
和 的夹角是锐角,则
的夹角是锐角,则 的取值范围是___ _.
的取值范围是___ _. 、
、 、
、 为同平面内具有相同起点的任意三个非零向量,且满足
为同平面内具有相同起点的任意三个非零向量,且满足 ,
, ,则
,则 的值一定等于( )
的值一定等于( )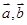 为非零向量,且
为非零向量,且

 ,求
,求 与
与 的夹角
的夹角 。
。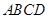 的顶点
的顶点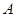 ,
,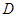 分别在
分别在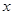 轴、
轴、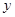 轴正半轴上移动,则
轴正半轴上移动,则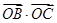 的最大值是( )
的最大值是( )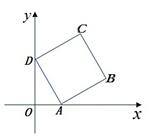



 的坐标.
的坐标. 中,
中, 分别是角
分别是角 所对的边
所对的边
 ,向量
,向量 ,若
,若 ,则实数
,则实数 的
的 
