题目内容
【题目】在
中，内角
，
，
的对边分别为
，
，
．若的面积为
，且
，
，则
外接圆的面积为____________
【答案】
【解析】
由余弦定理，三角形面积公式，同角三角函数基本关系式化简已知等式可得tanA=1，结合范围A∈（0，π），可得A的值，设△ABC外接圆的半径为R，由正弦定理可得R，利用圆的面积公式即可求解.
由余弦定理：a2=b2+c2-2bccosA，可得：2bccosA=b2+c2-a2=b2+c2-1，
又∵S=
bcsinA，可得4S=2bcsinA，
由4S=b2+c2-1，可得2bccosA=2bcsinA，可得tanA=1，
∵A∈（0，π），∴A=
，
设△ABC外接圆的半径为R，由正弦定理可得
∵a=1，A=，可得R= 
，∴△ABC外接圆的面积S=πR2=．
故答案为：．
练习册系列答案
相关题目
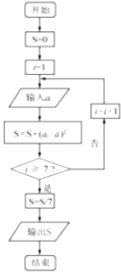
【题目】某人在连续7天的定点投篮的分数统计如下：在上述统计数据的分析中，一部分计算如右图所示的算法流程图（其中 
是这7个数据的平均数），则输出的S的值是（ ）
观测次数i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
观测数据ai | 5 | 6 | 8 | 6 | 8 | 8 | 8 |
A.1
B.
C.
D.
