题目内容
如图,四棱锥![]() 的底面
的底面![]() 为菱形,
为菱形,![]() 平面
平面![]() ,
,
![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点。
的中点。
(I)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求三棱锥![]() 的体积;
的体积;
(Ⅲ)求平面![]() 与平面
与平面![]() 所成的锐二面角大小的余弦值。
所成的锐二面角大小的余弦值。

(2)![]() (3)
(3)![]()
解析:
(I)连结BD,由已知得BD=2,
在正三角形BCD中,BE=EC,
![]() ,又
,又![]() ,
,
![]() ------------ 2分
------------ 2分
又![]() 平面
平面![]() ,
,
![]() , ------------3分
, ------------3分
![]() ,
,
![]() 平面PAD。 ------------4分
平面PAD。 ------------4分
(Ⅱ)![]() ,
,
且![]() , ------5分
, ------5分
![]() --------8分
--------8分
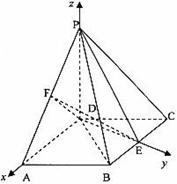 (Ⅲ)证法一:如图建立空间直角坐标系
(Ⅲ)证法一:如图建立空间直角坐标系![]() ,
,
则由(I)知平面![]() 的一个法向量为
的一个法向量为![]()
![]() ,
,
![]()
设平面PBC的法向量为![]() ,
,
由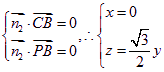
取![]() 得
得![]() ----------11分
----------11分
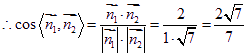 --------13分
--------13分
![]() 平面PAD与平面PBC所成的锐二面角大小的余弦值为
平面PAD与平面PBC所成的锐二面角大小的余弦值为![]() -------14分
-------14分
证法二:由(I)知![]() 平面
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() -------9分
-------9分
又![]()
![]() 平面
平面![]() 又
又![]() 平面
平面![]()
![]() 平面
平面![]() 平面
平面![]() --------10分
--------10分
![]() 就是平面
就是平面![]() 与平面
与平面![]() 所成二面角的平面角 ---------12分
所成二面角的平面角 ---------12分
![]() 在
在![]() 中,
中,![]()
![]() --------14分
--------14分

练习册系列答案
相关题目
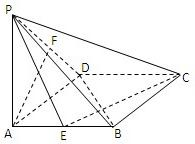 如图,四棱锥的底面为菱形,PA⊥底面ABCD,E、F分别是AB与PD的中点.
如图,四棱锥的底面为菱形,PA⊥底面ABCD,E、F分别是AB与PD的中点. 如图,四棱锥
如图,四棱锥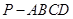 的底面
的底面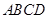 为矩形,且
为矩形,且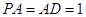 ,
,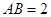 ,
,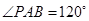 ,
,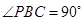 ,
,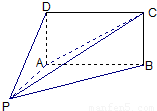
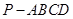 的底面
的底面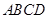 为矩形,且
为矩形,且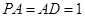 ,
,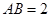 ,
, ,
,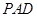
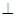 平面
平面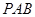 ;
;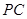 与平面
与平面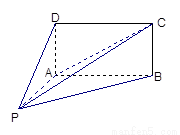
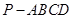 的底面
的底面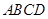 为菱形,
为菱形,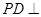 平面
平面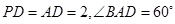 ,
,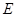 、
、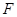 分别为
分别为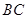 、
、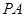 的中点。
的中点。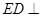 平面
平面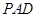 ;
; (Ⅱ)求三棱锥
(Ⅱ)求三棱锥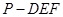 的体积;
的体积;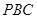 所成的锐二面角大小的余弦值。
所成的锐二面角大小的余弦值。