题目内容
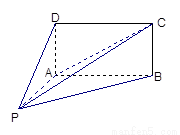
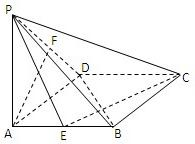
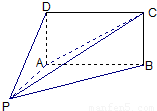
如图,四棱锥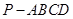 的底面
的底面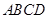 为矩形,且
为矩形,且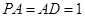 ,
,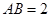 ,
, ,
,
(Ⅰ)求证:平面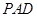
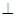 平面
平面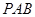 ;
;
(Ⅱ)求直线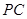 与平面
与平面 所成角的正弦值
所成角的正弦值
【答案】
(I)证明:由题意得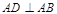 且
且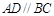
又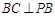 ,则
,则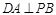 ……………………………3分
……………………………3分
则 平面
平面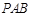 , 故平面
, 故平面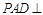 平面
平面 ………………6分
………………6分
(Ⅱ)解法1:

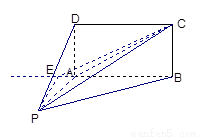
以点A为坐标原点,AB所在的直线为y轴建立空间直角坐标系如右图示,则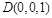 ,
,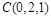 ,
,
可得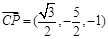 , ……………………………8分
, ……………………………8分
平面ABCD的单位法向量为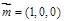 ,………10分
,………10分
设直线PC与平面ABCD所成角为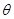 ,则
,则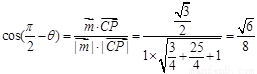 …13分
…13分
则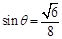 ,即直线PC与平面ABCD所成角的正弦值
,即直线PC与平面ABCD所成角的正弦值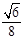 …………………………………14分
…………………………………14分
解法2:
由(I)知 平面
平面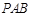 ,∵
,∵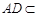 面
面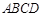
∴平面ABCD⊥平面PAB,
在平面PAB内,过点P作PE⊥AB,垂足为E,则PE⊥平面ABCD,连结EC,则∠PCE为直线PC与平面ABCD所成的角,在Rt△PEA中,∵∠PAE=60°,PA=1,∴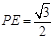 ,又
,又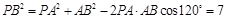 ∴
∴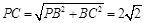
在Rt△PEC中 .
.
【解析】略

练习册系列答案
相关题目
 如图,四棱锥的底面为菱形,PA⊥底面ABCD,E、F分别是AB与PD的中点.
如图,四棱锥的底面为菱形,PA⊥底面ABCD,E、F分别是AB与PD的中点. 如图,四棱锥
如图,四棱锥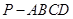 的底面
的底面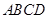 为矩形,且
为矩形,且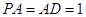 ,
,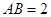 ,
,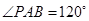 ,
,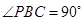 ,
,
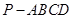 的底面
的底面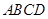 为菱形,
为菱形,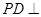 平面
平面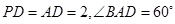 ,
,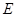 、
、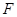 分别为
分别为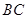 、
、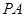 的中点。
的中点。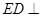 平面
平面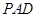 ;
; (Ⅱ)求三棱锥
(Ⅱ)求三棱锥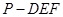 的体积;
的体积;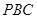 所成的锐二面角大小的余弦值。
所成的锐二面角大小的余弦值。