题目内容
已知 ,
, ,直线
,直线 与函数
与函数 、
、 的图象都相切,且与函数
的图象都相切,且与函数 的图象的切点的横坐标为
的图象的切点的横坐标为 .
.
(Ⅰ)求直线 的方程及
的方程及 的值;
的值;
(Ⅱ)若 (其中
(其中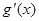 是
是 的导函数),求函数
的导函数),求函数 的最大值;
的最大值;
(Ⅲ)当 时,求证:
时,求证: .
.
(Ⅰ)直线 的方程为
的方程为 .
. .
.
(Ⅱ)当 时,
时, 取最大值,其最大值为2.
取最大值,其最大值为2.
(Ⅲ)
解析试题分析:(Ⅰ) ,
, .∴直线
.∴直线 的斜率为
的斜率为 ,且与函数
,且与函数 的图象的切点坐标为
的图象的切点坐标为 . ∴直线
. ∴直线 的方程为
的方程为 . 又∵直线
. 又∵直线 与函数
与函数 的图象相切,
的图象相切,
∴方程组 有一解. 由上述方程消去
有一解. 由上述方程消去 ,并整理得
,并整理得 ①
①
依题意,方程①有两个相等的实数根,
解之,得 或
或

 .
.
(Ⅱ)由(Ⅰ)可知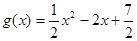 ,
,
 .
.  .
.
∴当 时,
时, ,当
,当 时,
时, .
.
∴当 时,
时, 取最大值,其最大值为2.
取最大值,其最大值为2.
(Ⅲ)  .
.  ,
,  ,
,  .
.
由(Ⅱ)知当 时,
时, ∴当
∴当 时,
时, ,
, . ∴
. ∴
考点:导数的几何意义,直线方程,利用导数研究函数的极值(最值),不等式证明问题。
点评:典型题,切线的斜率,等于在切点的导函数值。利用导数研究函数的极值,一般遵循“求导数、求驻点、研究导数的正负、确定极值”,利用“表解法”,清晰易懂。不等式的证明问题,往往通过构造函数,通过研究函数的最值达到目的。

练习册系列答案
相关题目
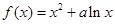 的图象在点
的图象在点 处的切线斜率为
处的切线斜率为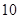 .
.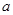 的值;
的值;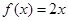 根的个数,证明你的结论;
根的个数,证明你的结论; ,使得曲线
,使得曲线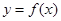 在该点附近的左、右的两部分分别位于曲线在该点处切线的两侧?若存在,求出点A的坐标;若不存在,说明理由.
在该点附近的左、右的两部分分别位于曲线在该点处切线的两侧?若存在,求出点A的坐标;若不存在,说明理由.
 ,试确定函数
,试确定函数 的单调区间;
的单调区间; ,且对于任意
,且对于任意 ,
, 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围; ,求证:
,求证: .
. (e为自然对数的底数).
(e为自然对数的底数). 的单调增区间;
的单调增区间; ≥
≥ 的解集为M,且集合
的解集为M,且集合 ,求实数t的取值范围.
,求实数t的取值范围. 在
在 与
与 时都取得极值
时都取得极值 的值与函数
的值与函数 的单调区间
的单调区间 ,不等式
,不等式 恒成立,求c的取值范围
恒成立,求c的取值范围 在(1,2)上是增函数,
在(1,2)上是增函数,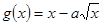 在(0,1)上是减函数。
在(0,1)上是减函数。 求
求 的值;
的值; 当
当 时,若
时,若 在
在 内恒成立,求实数
内恒成立,求实数 的取值范围;
的取值范围; 求证:方程
求证:方程 在
在 内有唯一解.
内有唯一解. .
. 的单调区间;
的单调区间; 时,判断
时,判断 和
和 的大小,并说明理由;
的大小,并说明理由; 时,关于
时,关于 的方程:
的方程: 在区间
在区间 上总有两个不同的解.
上总有两个不同的解. .
. 时,求曲线
时,求曲线 在点
在点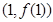 处的切线方程;
处的切线方程;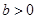 ,
, 在区间
在区间 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围. 。
。 的单调递减区间;
的单调递减区间; 的切线方程;
的切线方程; 上的最大值与最小值。
上的最大值与最小值。