题目内容
用反证法证明:已知 ,
, ,
, ,求证:
,求证: ,
, ,
,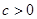 .
.
证明详见解析.
解析试题分析:根据应用反证法证明命题的一般步骤:先假设原命题的结论不成立,由此找出矛盾,从而肯定结论.本题先假设 不都是正数,结合
不都是正数,结合 可知三个数中必有两个为负数,一个为正数,根据本题中的条件
可知三个数中必有两个为负数,一个为正数,根据本题中的条件 互相进行轮换后都没有变化,从而不妨设
互相进行轮换后都没有变化,从而不妨设 ,进而根据条件得出
,进而根据条件得出 ,由此推导出
,由此推导出 ,这与条件
,这与条件 矛盾,从而可肯定原结论正确.
矛盾,从而可肯定原结论正确.
假设 不都是正数 1分
不都是正数 1分
由 可知,这三个数中必有两个为负数,一个为正数 2分
可知,这三个数中必有两个为负数,一个为正数 2分
不妨设
则由 可得
可得 4分
4分
又 ,∴
,∴ 5分
5分 即
即 7分
7分
∵ ,∴
,∴
即 9分
9分
这与已知 矛盾
矛盾
所以假设不成立.因此 成立 10分
成立 10分
考点:反证法.

练习册系列答案
相关题目
 个小正方形.
个小正方形.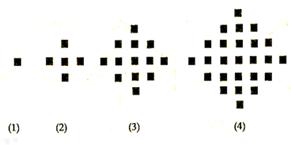
 ;
; 与
与 的关系式,
的关系式, 的表达式.
的表达式. 是一个自然数,
是一个自然数, 是
是 :
: 是自然数,
是自然数, (
( ,
, ).
). ,
, ;
; ,求证:
,求证: ;
; 时,求证:存在
时,求证:存在 ,使得
,使得 .
. 的展开式中,
的展开式中, 的系数为
的系数为 ,
, 的系数为
的系数为 ,其中
,其中
 ,对
,对 恒成立?证明你的结论.
恒成立?证明你的结论. +
+ +…+
+…+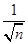 ,试比较f(n)与
,试比较f(n)与 的大小.
的大小. n∈N?),g(n)=2(
n∈N?),g(n)=2( -1)(n∈N?).
-1)(n∈N?). 为有理数集,
为有理数集, 为实数集,
为实数集, 为复数集);
为复数集); 类比推出
类比推出
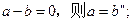
 类比推出
类比推出 ,若
,若
 类比推出
类比推出 其中类比结论正确的序号是_____________(写出所有正确结论的序号)
其中类比结论正确的序号是_____________(写出所有正确结论的序号)