题目内容
已知直线m经过点P(-3,-
),被圆O:x2+y2=25所截得的弦长为8,
(1)求此弦所在的直线方程;
(2)求过点P的最短弦和最长弦所在直线的方程.
| 3 |
| 2 |
(1)求此弦所在的直线方程;
(2)求过点P的最短弦和最长弦所在直线的方程.
(12 分)
(1)由题意易知:圆心O到直线m到的距离为3.
设m所在的直线方程为:y+
=k(x+3),即2kx-2y+6k-3=0.
由题意易知:圆心O到直线m到的距离为3,
即
=3.解得k=-
此时直线m为:3x+4y+15=0,
而直线x=-3显然也符合题意.
故直线m为:3x+4y+15=0或x=-3.
(2)过点P的最短弦就是圆心与P连线垂直的直线,k=-
=-2,
所以,过点P的最短弦所在直线的方程为:y+
=-2(x+3),
即:4x+2y+15=0;
最长弦就是直线经过圆心所在直线,k=
=
.
所以,过点P的最长弦所在直线的方程为:y+
=
(x+3).
即:x-2y=0.
(1)由题意易知:圆心O到直线m到的距离为3.
设m所在的直线方程为:y+
| 3 |
| 2 |
由题意易知:圆心O到直线m到的距离为3,
即
| |6k-3| | ||
|
| 3 |
| 4 |
此时直线m为:3x+4y+15=0,
而直线x=-3显然也符合题意.
故直线m为:3x+4y+15=0或x=-3.
(2)过点P的最短弦就是圆心与P连线垂直的直线,k=-
| -3-0 | ||
-
|
所以,过点P的最短弦所在直线的方程为:y+
| 3 |
| 2 |
即:4x+2y+15=0;
最长弦就是直线经过圆心所在直线,k=
-
| ||
| -3 |
| 1 |
| 2 |
所以,过点P的最长弦所在直线的方程为:y+
| 3 |
| 2 |
| 1 |
| 2 |
即:x-2y=0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
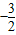 ),被圆O:x2+y2=25所截得的弦长为8,
),被圆O:x2+y2=25所截得的弦长为8, ),被圆O:x2+y2=25所截得的弦长为8,
),被圆O:x2+y2=25所截得的弦长为8,