题目内容
15.已知向量$\overrightarrow{a}$=(sinx,cosx),$\overrightarrow{b}$=(sinx,sinx),$\overrightarrow{c}$=(-1,0).(1)求函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$的周期和单调减区间;
(2)若x∈[-$\frac{3π}{8}$,$\frac{π}{4}$],函数f(x)=λ$\overrightarrow{a}$•$\overrightarrow{b}$的最大值为$\frac{1}{2}$,求实数λ的值.
分析 (1)由数量积的定义和三角函数公式化简可得f(x)=2cos(2x+)+3,易得周期和单调区间;
(2)求得函数f(x)=λ$\overrightarrow{a}$•$\overrightarrow{b}$,利用三角函数的诱导公式进行化简,转化为三角函数在定区间上的最值,即可求得结果.
解答 解:(1)因为f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$=sin2x+sinxcosx=$\frac{1-cos2x}{2}$+$\frac{1}{2}$sin2x=$\frac{\sqrt{2}}{2}$sin(2x-$\frac{π}{4}$)+$\frac{1}{2}$,
所以周期T=$\frac{2π}{2}=π$,由2kπ+$\frac{π}{2}$≤2x-$\frac{π}{4}$≤2kπ$+\frac{3π}{2}$,k∈Z,解得单调减区间为:[k$π+\frac{3π}{8}$,k$π+\frac{7π}{8}$],k∈Z.
(2)因为f(x)=λ$\overrightarrow{a}$•$\overrightarrow{b}$=λ$\frac{\sqrt{2}}{2}$sin(2x-$\frac{π}{4}$)+$\frac{1}{2}$λ=$\frac{λ}{2}$[1+$\sqrt{2}$sin(2x-$\frac{π}{4}$)],
因为x∈[-$\frac{3π}{8}$,$\frac{π}{4}$],
所以2x-$\frac{π}{4}$∈[-$\frac{π}{2}$,$\frac{π}{4}$],
当λ>0时,fmax(x)=$\frac{λ}{2}$(1+1)=$\frac{1}{2}$,即λ=$\frac{1}{2}$,
当λ<0时,fmax(x)=$\frac{λ}{2}$(1-$\sqrt{2}$)=$\frac{1}{2}$,即λ=-1-$\sqrt{2}$,
所以λ=$\frac{1}{2}$或λ=-1-$\sqrt{2}$.
点评 此题是个中档题.考查向量的数量积的坐标运算,和三角函数的诱导公式和三角函数在定区间上的最值等基础知识,同时也考查了学生灵活应用知识分析解决问题的能力.

| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
(2)求回归直线方程;
(3)据此估计广告费用为10销售收入y的值.
参考公式:最小二乘法得$\left\{\begin{array}{l}{\widehat{b}=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n\overline{{x}^{2}}}}\\{\widehat{a}=\overline{y}-\widehat{b}\overline{x}}\end{array}\right.$其中:$\widehat{b}$是回归方程的斜率,$\widehat{a}$是截距.
| A. | 60° | B. | 45° | C. | 90° | D. | 30° |
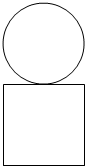 某几何体的正视图如图所示,则该几何体的俯视图不可能的是( )
某几何体的正视图如图所示,则该几何体的俯视图不可能的是( )| A. | 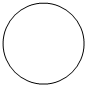 | B. |  | C. | 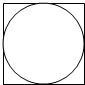 | D. |  |