题目内容
已知a1,a2, …,an都是正实数，且a1+a2+…+an=1.求证：
≥
.
思路分析：已知条件中a1+a2+…+an=1,可以看作“1”的代换，而要证的不等式的左侧，“数式”已经可以看出来，为, …,所以a1+a2+…+an=1.应扩大2倍后再利用，本题还可以利用其他的方法证明.
证法一：根据柯西不等式，得
左边=
=［(a1+a2)+(a2+a3)+(a3+a4)+ …+(an-1+an)+(an+a1)］×
［(
)2+(
)2
+(
)2+…+(
)2+(
)2］×
=［(
)2+(
)2+…+(
)2+(
)2］×［(
)2+(
)2+…+（
）2+(
)2］×
≥［(
×
)+(
×
)+…+(
×
)+(
×
)］2×
=(a1+a2+…+an)2×
=
=右边.
∴原不等式成立.
证法二：∵a∈R+,则a+
≥2,
a≥2-
.
利用上面的结论，知
同理，有
,
…
,
.
以上式子相加整理，得
≥
（a1+a2+…+an）=
.
证法三：对于不等式左边的第一个分式
,配制辅助式k(a1+a2)，k为待定的正数，这里取k=
,则
(a1+a2)≥
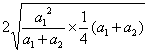=a1.
同理，
(a2+a3)≥a2.
……
(an-1+an)≥an-1，
(an+a1)≥an.
以上式子相加整理，得
≥
(a1+a2+…+an).
∵a1+a2+…+an=1,
∴
≥
.
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
导学与测试系列答案
相关题目