题目内容
19.已知正六边形ABCDEF,$\overrightarrow{AC}$=$\overrightarrow{a}$,$\overrightarrow{BD}$=$\overrightarrow{b}$,用$\overrightarrow{a}$,$\overrightarrow{b}$表示向量$\overrightarrow{DE}$,$\overrightarrow{AD}$.分析 作出图形,根据相似三角形可得到$\frac{AG}{CG}=\frac{2}{1}$,从而得到$\overrightarrow{AG}=\frac{2}{3}\overrightarrow{a}$,而同理可得到$\overrightarrow{GD}=\frac{2}{3}\overrightarrow{b}$,这样根据向量加法及减法的几何意义即可表示出$\overrightarrow{AD},\overrightarrow{DE}$.
解答 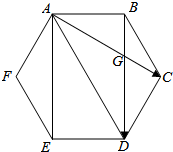 解:如图,
解:如图,
设AC交BD于G,则:$\frac{AG}{CG}=\frac{AD}{CB}=\frac{2}{1}$;
∴$AG=\frac{2}{3}AC$;
∴$\overrightarrow{AG}=\frac{2}{3}\overrightarrow{a}$,同理$\overrightarrow{GD}=\frac{2}{3}\overrightarrow{b}$;
∴$\overrightarrow{AD}=\overrightarrow{AG}+\overrightarrow{GD}=\frac{2}{3}\overrightarrow{a}+\frac{2}{3}\overrightarrow{b}$,连接AE,则$\overrightarrow{AE}=\overrightarrow{BD}=\overrightarrow{b}$;
∴$\overrightarrow{DE}$=$\overrightarrow{AE}-\overrightarrow{AD}=\overrightarrow{b}-(\frac{2}{3}\overrightarrow{a}+\frac{2}{3}\overrightarrow{b})$=$-\frac{2}{3}\overrightarrow{a}+\frac{1}{3}\overrightarrow{b}$.
点评 考查正六边形的边及对角线的关系,三角形相似的比例关系,数乘的几何意义,以及向量加法、减法的几何意义.

 如图所示,点A、B是圆O上的两点,∠AOB=60°,点D是圆O上异于A,B的任意一点,若$\overrightarrow{OD}$=μ$\overrightarrow{OA}$+λ$\overrightarrow{OB}$,则μ+λ的最大值为$\frac{2\sqrt{3}}{3}$.
如图所示,点A、B是圆O上的两点,∠AOB=60°,点D是圆O上异于A,B的任意一点,若$\overrightarrow{OD}$=μ$\overrightarrow{OA}$+λ$\overrightarrow{OB}$,则μ+λ的最大值为$\frac{2\sqrt{3}}{3}$.
 从高出海平面h=30米的小岛看正东方向有一只船B俯角为30°.看正南方向一只船A俯角为45°,求两船间的距离.
从高出海平面h=30米的小岛看正东方向有一只船B俯角为30°.看正南方向一只船A俯角为45°,求两船间的距离.