Question

【题目】如图，在四棱锥中，底面是边长为的正方形， 为等边三角形， ， 分别是， 的中点， .

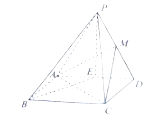
（Ⅰ）求证：平面平面；

（Ⅱ）求点到平面的距离.

Answer 1

【答案】(Ⅰ)证明见解析；(Ⅱ) .

【解析】试题分析：(Ⅰ)根据正三角形的性质可得，由勾股定理可得，由线面垂直的判定定理可得平面，从而根据面面垂直的判定定理可得平面平面；（Ⅱ）根据平面，可得，结合，可得平面，故为三棱锥的高，根据平面几何知识分别算出与的面积，由得， 可得点到平面的距离.

试题解析：（Ⅰ）由题意知，正的边长为， 点为的中点，.

， .

在正方形中， 为的中点，边长为，则.

在中， ， .

又， 平面.

又平面， 平面 平面；

（Ⅱ）由题意得， ， 为等边三角形，则， .

平面， .

， 平面.

故为三棱锥的高.

.

又 是的中点， .

在正方形中， ，则在中，满足， 为直角三角形， .

.

设点到平面的距离为，由得， ，解得.