题目内容
10.设f(x)=a0xn+a1xn-1+…+an-1x+an(n∈N*),则f′(0)=( )| A. | an | B. | an-1 | C. | a0 | D. | 0 |
分析 先求导再计算f′(0)即可.
解答 解:∵设f(x)=a0xn+a1xn-1+…+an-1x+an(n∈N*),
∴f′(x)=na0xn-1+(n-1)a1xn-2+…+an-1(n∈N*),
∴f′(0)=an-1,
故选:B.
点评 本题主要导数的运算,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.下列各式中正确的是( )
| A. | tan735°>tan800° | B. | tan1>-tan2 | C. | tan$\frac{5π}{7}$<tan$\frac{4π}{7}$ | D. | tan$\frac{9π}{8}$<tan$\frac{π}{7}$ |
17.下列各角与320°角终边相同的是( )
| A. | 45° | B. | -50° | C. | -40° | D. | 920° |
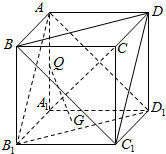 如图,ABCD-A1B1C1D1是棱长为a的正方体,有下列说法:
如图,ABCD-A1B1C1D1是棱长为a的正方体,有下列说法: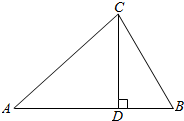 “如图,在△ABC中,AC>BC,CD是AB边上的高,求证:∠ACD>∠BCD”.
“如图,在△ABC中,AC>BC,CD是AB边上的高,求证:∠ACD>∠BCD”.