题目内容
1.求使1+2+3+4+5+…+n>100成立的最小自然数n的值,并画出程序框图.分析 分析题目中的要求,发现这是一个累加型的问题,用循环结构来实现,累加的初始值为1,累加值每一次增加1,退出循环的条件是累加结果>100,把握住以上要点不难得到程序框图.
解答 解:程序框图如下: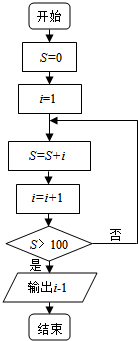
点评 可利用循环语句来实现数值的累加(乘)常分如下步骤:①观察S的表达式分析,循环的初值、终值、步长②观察每次累加的值的通项公式③在循环前给累加器和循环变量赋初值,累加器的初值为0,累乘器的初值为1,环变量的初值同累加(乘)第一项的相关初值④在循环体中要先计算累加(乘)值,如果累加(乘)值比较简单可以省略此步,累加(乘),给循环变量加步长⑤输出累加(乘)值.

练习册系列答案
相关题目
4.已知函数f(x)=asin(πx+α)+bcos(πx+β),且f(2014)=3,则f(2015)的值是( )
| A. | -1 | B. | -2 | C. | -3 | D. | 1 |
9.抛物线y=-$\frac{1}{4}{x}^{2}$的焦点到准线的距离为( )
| A. | 2 | B. | 1 | C. | 4 | D. | 3 |
13. 一个几何体的三视图如图所示,其俯视图为一个半圆和一个等腰梯形,则该几何体的体积为( )
一个几何体的三视图如图所示,其俯视图为一个半圆和一个等腰梯形,则该几何体的体积为( )
 一个几何体的三视图如图所示,其俯视图为一个半圆和一个等腰梯形,则该几何体的体积为( )
一个几何体的三视图如图所示,其俯视图为一个半圆和一个等腰梯形,则该几何体的体积为( )| A. | $\frac{\sqrt{2}}{3}$π+$\frac{\sqrt{6}}{4}$ | B. | $\frac{\sqrt{2}}{3}$π+$\frac{\sqrt{6}}{2}$ | C. | $\frac{2\sqrt{2}}{3}$π+$\frac{\sqrt{6}}{4}$ | D. | $\frac{2\sqrt{2}}{3}$π+$\frac{\sqrt{6}}{2}$ |
10.在△ABC中,AC=20,∠A=90°,S△ABC=120,则AB=( )
| A. | 6 | B. | 12 | C. | 24 | D. | 3 |