题目内容
2．对于数列1，2，22，23，…，2n，…（1）该数列的首项和公比分别是多少？
（2）把该数列的前n项和Sn=1+2+22+…+2n①
两边同乘以公比2得：2Sn=2+22+23+…+2n+1②
这两个等式的右边有何相同点？若用②式减去①式，会有什么结果？
分析 利用等比数列的定义及求和方法，即可得出结论．
解答 解：（1）该数列的首项是1、公比是2；
（2）把该数列的前n项和Sn=1+2+22+…+2n①
两边同乘以公比2得：2Sn=2+22+23+…+2n+1②
这两个等式的右边有n-1个相同项，若用②式减去①式，Sn=2n+1-1．
点评 本题考查等比数列的定义及求和方法，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
17．函数y=cos（sin|x|）的图象大致是（ ）
| A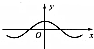． |  | B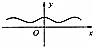． |  | C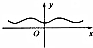． |  | D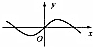． |  |