Question

2．直线2x+y-10=0与不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x-y≥-2}\\{4x+3y≤20}\end{array}\right.$表示的平面区域的公共点有（　　）

• A． 0 个
• B． 1个
• C． 2个
• D． 无数个

Answer 1

分析 画出约束条件表示的可行域，利用目标函数与可行域的交点，判断即可．

解答 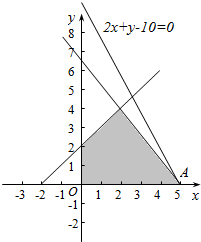解：不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x-y≥-2}\\{4x+3y≤20}\end{array}\right.$以及2x+y-10=0表示的可行域与直线如图：显然在与可行域只有一个交点A（5，0）．
故选：B．

点评 本题考查线性规划的应用，考查计算能力以及作图能力．