题目内容
【题目】如图,直角坐标系中,圆的方程为![]() ,
,![]() ,
,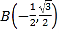 ,
,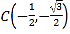 为圆上三个定点,某同学从
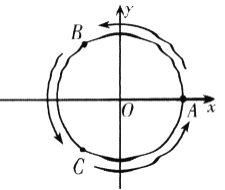
为圆上三个定点,某同学从![]() 点开始,用掷骰子的方法移动棋子.规定:①每掷一次骰子,把一枚棋子从一个定点沿圆弧移动到相邻下一个定点;②棋子移动的方向由掷骰子决定,若掷出骰子的点数为偶数,则按图中箭头方向移动;若掷出骰子的点数为奇数,则按图中箭头相反的方向移动.设掷骰子
点开始,用掷骰子的方法移动棋子.规定:①每掷一次骰子,把一枚棋子从一个定点沿圆弧移动到相邻下一个定点;②棋子移动的方向由掷骰子决定,若掷出骰子的点数为偶数,则按图中箭头方向移动;若掷出骰子的点数为奇数,则按图中箭头相反的方向移动.设掷骰子![]() 次时,棋子移动到
次时,棋子移动到![]() ,
,![]() ,
,![]() 处的概率分别为
处的概率分别为![]() ,
,![]() ,
,![]() .例如:掷骰子一次时,棋子移动到
.例如:掷骰子一次时,棋子移动到![]() ,
,![]() ,
,![]() 处的概率分别为
处的概率分别为![]() ,
,![]() ,
,![]() .
.
(1)分别掷骰子二次,三次时,求棋子分别移动到![]() ,
,![]() ,
,![]() 处的概率;
处的概率;
(2)掷骰子![]() 次时,若以
次时,若以![]() 轴非负半轴为始边,以射线
轴非负半轴为始边,以射线![]() ,
,![]() ,
,![]() 为终边的角的余弦值记为随机变量
为终边的角的余弦值记为随机变量![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)记![]() ,
,![]() ,
,![]() ,其中
,其中![]() .证明:数列
.证明:数列![]() 是等比数列,并求
是等比数列,并求![]() .
.
【答案】(1)详见解析;(2)详见解析;(3)证明详见解析,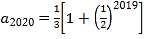 .
.
【解析】
(1)由概率的乘法公式,可得所求值;
(2)随机变量![]() 的可能数值为1,
的可能数值为1,![]() ,结合(1)运用概率的乘法公式,可随机变量
,结合(1)运用概率的乘法公式,可随机变量![]() 的分布列和期望;
的分布列和期望;
(3)易知![]() ,即
,即![]() ,由条件推得
,由条件推得![]() ,利用构造法可得
,利用构造法可得![]() ,从而求得
,从而求得![]() 的值.
的值.
(1)![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]()
综上,
棋子位置 掷骰子次数 |
|
|
|
2 |
|
|
|
3 |
|
|
|
(2)随机变量![]() 的可能数值为1,
的可能数值为1,![]() .
.
综合(1)得
![]()
![]() ,
,
![]()
![]() ,
,
故随机变量![]() 的分布列为
的分布列为
|
|
|
|
|
|
![]() .
.
(3)易知![]() ,因此,
,因此,![]()
而当![]() 时,
时,![]() ,
,
又![]() ,
,
即![]() .
.
因此![]()
![]() ,
,
故![]()
![]()
即数列![]() 是以
是以![]() 为首项,公比为
为首项,公比为![]() 的等比数列.
的等比数列.
所以![]() ,
,
又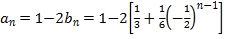
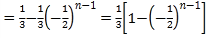
故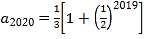 .
.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目