题目内容
已知f(log2x)=| x2-2x+1 |
(1)求f(x)的解析式;
(2)画出f(x)的图象,并求出单调区间;
(3)讨论f(x)与f(x+1)的大小.
分析:(1)根据f(log2x)=
=|x-1|,利用换元法令t=log2x,则x=2t,代入f(log2x)=
,即可求得f(x)的解析式;
(2)根据(1),利用函数图象 的平移和对称变换画出画出f(x)的图象,并根据图象求出单调区间;
(3)令f(x)=f(x+1)求出x的值,分三种情况讨论f(x)与f(x+1)的大小.
| x2-2x+1 |
| x2-2x+1 |
(2)根据(1),利用函数图象 的平移和对称变换画出画出f(x)的图象,并根据图象求出单调区间;
(3)令f(x)=f(x+1)求出x的值,分三种情况讨论f(x)与f(x+1)的大小.
解答: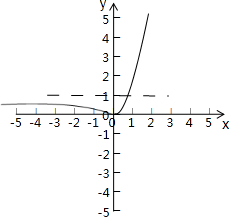 解:(1)f(log2x)=
解:(1)f(log2x)=
=|x-1|,
令t=log2x,则x=2t,
∴f(t)=|2t-1|,
即f(x)=|2x-1|;
(2)根据函数图象知,f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增;
(3)f(x+1)=|2x+1-1|;
1°当x>log2
时,有|2x+1-1|>|2x-1|,即f(x)<f(x+1);
2°当x=log2
时,有|2x+1-1|=|2x-1|,即f(x)=f(x+1);
3°当x<log2
时,有|2x+1-1|<|2x-1|,即f(x)>f(x+1).
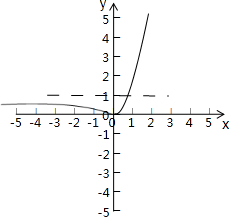 解:(1)f(log2x)=
解:(1)f(log2x)=| x2-2x+1 |
令t=log2x,则x=2t,
∴f(t)=|2t-1|,
即f(x)=|2x-1|;
(2)根据函数图象知,f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增;
(3)f(x+1)=|2x+1-1|;
1°当x>log2
| 2 |
| 3 |
2°当x=log2
| 2 |
| 3 |
3°当x<log2
| 2 |
| 3 |
点评:此题是个中档题.考查了利用换元法求函数解析式和函数图象的变换,体现了数形结合的思想,以及学生分析解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目