题目内容
如图，已知锐二面角α-l-β，A为α面内一点，A到β的距离为
，到l的距离为4，则二面角α-l-β的大小为
- A.30°
- B.45°
- C.60°
- D.90°
C
分析：过A作AO⊥β垂足为O，作AH⊥l，垂足为H，连接HO，∠AHO为锐二面角α-l-β的平面角，在直角△AHO中求解即可．
解答：过A作AO⊥β垂足为O，则AO=，作AH⊥l，垂足为H，则AH=4．连接HO，
?l⊥面AOH，∴l⊥OH．∠AHO为锐二面角α-l-β的平面角，
在直角△AHO中，sin∠AHO=
=
，∠AHO=60°．
故选C．
点评：本题考查二面角的大小度量，考查转化、空间想象、计算能力．本题找出∠AHO为锐二面角α-l-β的平面角是关键．
分析：过A作AO⊥β垂足为O，作AH⊥l，垂足为H，连接HO，∠AHO为锐二面角α-l-β的平面角，在直角△AHO中求解即可．
解答：过A作AO⊥β垂足为O，则AO=
，作AH⊥l，垂足为H，则AH=4．连接HO，?l⊥面AOH，∴l⊥OH．∠AHO为锐二面角α-l-β的平面角，在直角△AHO中，sin∠AHO=
=，∠AHO=60°．故选C．
点评：本题考查二面角的大小度量，考查转化、空间想象、计算能力．本题找出∠AHO为锐二面角α-l-β的平面角是关键．
练习册系列答案
相关题目
如图，已知直角梯形A1所在的平面垂直于平面B1，C1，D1，AB1?．
如图，已知锐二面角α-l-β，A为α面内一点，A到β的距离为
如图，已知△ABCD中，∠BCD=90°，AB⊥平面BCD，BC=2，CD=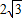
，到l的距离为4，则二面角α-l-β的大小为（ ）