题目内容
已知曲线C1:y=x2与C2:y=?-(x-2)2,若直线l与C1、C2都相切,求直线l的方程.
解法一:设直线l与两曲线的切点的坐标分别为A(a,a2),B(b,-(b-2)2).?
因为两曲线对应函数的导函数分别为y1′=2x,y2′=-2(x-2).?
所以在A、B两点处直线的斜率分别为y1′|x=a=2a,y2′|x=b=-2(b-2).?
由题意![]() =2a=-2b+4,?
=2a=-2b+4,?
即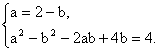 解得
解得![]()
所以A(2,4)或(0,0),切线的斜率k=4或0,?
从而切线方程为y=4x-4或y=0.?
解法二:设l与C1、C2的切点的横坐标分别为a、b,直线l的斜率为k.?
根据题意y1′=2x,y2′=-2(x-2),y1′|x=a=2a,y2′|x=b=-2(b-2).?
由k=2a=-2b+4,得a=![]() ,b=
,b=![]() .?
.?
设l与C1、C2的切点坐标分别为(![]() ),(
),(![]() ),则k=
),则k=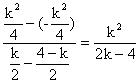 . 解得k=0或4.?
. 解得k=0或4.?
故所求切线方程为y=4x-4或y=0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
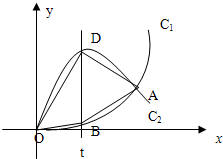 如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x3+3x(x≥0)交于O,A,直线x=
如图,已知曲线C1:y=x3(x≥0)与曲线C2:y=-2x3+3x(x≥0)交于O,A,直线x=