Question

设矩阵M是把坐标平面上的点的横坐标伸长到原来的3倍，纵坐标伸长到原来的2倍的伸压变换矩阵．
（1）求逆矩阵M^-1；
（2）求椭圆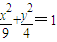在矩阵M^-1作用下变换得到的新曲线的方程．

Answer 1

【答案】分析：（1）根据已知条件，求出矩阵M，由M•M^-1=E，求出M^-1．
（2）设椭圆上任意一点（x，y），变换后的坐标（x′，y′），根据逆变换公式，知道之间的关系，代入，即可求出新曲线方程．
解答：解：（1）．（5分）
（2）任意选取椭圆上的一点P（x，y），它在矩阵
对应的变换下变为P'（x′，y′），则有，故．
又因为点P在椭圆上，所以，即有，
因此x^'2+y^'2=1．
从而椭圆在M^-1的作用下的新曲线的方程为x²+y²=1．（10分）
点评：本题主要考查逆矩阵、逆变换及其计算能力，难度比较大，做题要仔细．