题目内容
若实数m,n满足4m-3n=10,则m2+n2的最小值为分析:求m2+n2的最小值可先求
的最小值,然后转化成4m-3n=10上点(m,n)到原点的距离的最小值,然后结合图象可知当过原点的直线与直线4m-3n=10垂直时,原点到点(m,n)的距离最小,即可求出所求.
| (m-0)2+(n-0)2 |
解答:解:欲求m2+n2的最小值可先求
的最小值
而
表示4m-3n=10上点(m,n)到原点的距离
当过原点的直线与直线4m-3n=10垂直时,原点到点(m,n)的距离最小
(
)min=2
∴m2+n2的最小值为4
故答案为:4.
| (m-0)2+(n-0)2 |

而
| (m-0)2+(n-0)2 |
当过原点的直线与直线4m-3n=10垂直时,原点到点(m,n)的距离最小
(
| (m-0)2+(n-0)2 |
∴m2+n2的最小值为4
故答案为:4.
点评:本题主要考查了函数的最值及其几何意义,以及转化和数形结合的数学思想,属于基础题.

练习册系列答案
相关题目
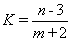 的最大值和最小值.
的最大值和最小值.  的最大值和最小值.
的最大值和最小值.