��Ŀ����
����Ŀ��ijУѧ���Ὺչ��һ�ι����������������ʾ������ʵ�������֯����ѧ���ɲ��ڼ�������С�������ȡ�˹�50����������ʾ�����.���������ѧ������ʾ����������ͳ�ƣ���������һ���������Ƿ�֪�������������֪����֪�������ĵ�����ͳ�����±���
���䣨�꣩ |
|
|
|
|
|
|
Ƶ�� |
|
| 14 | 12 | 8 | 6 |
֪�������� | 3 | 4 | 8 | 7 | 3 | 2 |
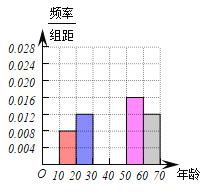
��1�����ϱ��е�![]() ��ֵ������ȫ��ͼ��ʾ�ĵ�Ƶ��ֱ��ͼ��
��ֵ������ȫ��ͼ��ʾ�ĵ�Ƶ��ֱ��ͼ��
��2���ڱ�����ľ����У�����������![]() �ľ����и����ѡȡ1�˲μ���������֪ʶ��������ѡ�е������н���һ�˲�֪������������ĸ���.
�ľ����и����ѡȡ1�˲μ���������֪ʶ��������ѡ�е������н���һ�˲�֪������������ĸ���.
���𰸡���1��m=4��n=6��ͼ������ ��2��![]()
��������
��1�����ȷֱ����![]() ��
��![]() ��Ƶ�ʣ��ټ���
��Ƶ�ʣ��ټ���![]() ���ɣ�����
���ɣ�����![]() ��ֵ���ɲ�ȫƵ�ʷֲ�ֱ��ͼ.
��ֵ���ɲ�ȫƵ�ʷֲ�ֱ��ͼ.
��2�������������![]() ��
��![]() �ľ����и����ѡȡ1�˵����л����¼������ҵ����н���һ�˲�֪������������Ļ����¼��������ɹŵ����ʽ�����������.
�ľ����и����ѡȡ1�˵����л����¼������ҵ����н���һ�˲�֪������������Ļ����¼��������ɹŵ����ʽ�����������.
��1��������![]() ��Ƶ��
��Ƶ��![]() ��
��
������![]() ��Ƶ��Ϊ
��Ƶ��Ϊ![]() .
.
Ƶ��ֱ��ͼ��ͼ��ʾ��

��2��������������![]() �ľ���Ϊ
�ľ���Ϊ![]() �����о���
�����о���![]() ��֪���������������
��֪���������������
����������![]() �ľ���Ϊ
�ľ���Ϊ![]() �����о���
�����о���![]() ��֪�������������.
��֪�������������.
��������![]() ��
��![]() �ľ����и����ѡȡ1�˵����л����¼��У�
�ľ����и����ѡȡ1�˵����л����¼��У�
![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��![]() �������¼���
�������¼���
���н���һ�˲�֪������������Ļ����¼�����![]() ����
����
���ԣ�ѡ�е������н���һ�˲�֪������������ĸ���![]() .
.