题目内容
已知等比数列 .
.(1)求c的值并求数列{an}的通项公式;
(2)若bn=n•an,求数列{bn}的前n项和Tn.
【答案】分析:(1)由等比数列 ,分别求出a1,a2,a3,由此利用等比中项能求出c和数列{an}的通项公式.
,分别求出a1,a2,a3,由此利用等比中项能求出c和数列{an}的通项公式.
(2)由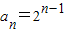 ,知bn=n•an=n•2n-1,由此利用错位相减法能求出数列{bn}的前n项和Tn.
,知bn=n•an=n•2n-1,由此利用错位相减法能求出数列{bn}的前n项和Tn.
解答:解:(1)∵等比数列 ,
,
∴a1=S1=2-c,
a2=S2-S1=(4-c)-(2-c)=2,
a3=S3-S2=(8-c)-(4-c)=4,
∵{an}是等比数列,
∴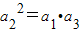 ,即22=(2-c)×4,
,即22=(2-c)×4,
解得c=1.
∵q=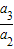 =
= =2.a1=2-1=1,
=2.a1=2-1=1,
∴an=2n-1.
(2)∵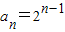 ,
,
∴bn=n•an=n•2n-1,
∴Tn=1+2•2+3•2n+…+n•2n-1,①
∴2Tn=1•2+2•22+…+(n-1)•2n-1+n•2n,②
①-②,得-Tn=1+2+22+…+2n-1-n•2n
=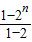 -n•2n
-n•2n
=2n-1-n•2n,
∴Tn=(n-1)•2n+1.
点评:本题考查数列的通项公式和前n项和的求法,解题时要认真审题,仔细解答,注意错位相减法的合理运用.
 ,分别求出a1,a2,a3,由此利用等比中项能求出c和数列{an}的通项公式.
,分别求出a1,a2,a3,由此利用等比中项能求出c和数列{an}的通项公式.(2)由
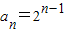 ,知bn=n•an=n•2n-1,由此利用错位相减法能求出数列{bn}的前n项和Tn.
,知bn=n•an=n•2n-1,由此利用错位相减法能求出数列{bn}的前n项和Tn.解答:解:(1)∵等比数列
 ,
,∴a1=S1=2-c,
a2=S2-S1=(4-c)-(2-c)=2,
a3=S3-S2=(8-c)-(4-c)=4,
∵{an}是等比数列,
∴
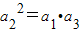 ,即22=(2-c)×4,
,即22=(2-c)×4,解得c=1.
∵q=
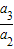 =
= =2.a1=2-1=1,
=2.a1=2-1=1,∴an=2n-1.
(2)∵
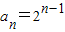 ,
,∴bn=n•an=n•2n-1,
∴Tn=1+2•2+3•2n+…+n•2n-1,①
∴2Tn=1•2+2•22+…+(n-1)•2n-1+n•2n,②
①-②,得-Tn=1+2+22+…+2n-1-n•2n
=
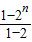 -n•2n
-n•2n=2n-1-n•2n,
∴Tn=(n-1)•2n+1.
点评:本题考查数列的通项公式和前n项和的求法,解题时要认真审题,仔细解答,注意错位相减法的合理运用.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 满足
满足 .
. 的前15项的和
的前15项的和 ;
; 满足
满足 ,
, ,求数列
,求数列 的前
的前 项的和
项的和
 .
.