题目内容
若二次函数f(x)=ax2+bx+c,(a<0)满足f(4)=f(1),那么
- A.f(-1)=f(5)
- B.f(-1)>f(5)
- C.f(-1)<f(5)
- D.f(-1)与f(5)的大小关系不能确定
C
分析:根据已知中二次函数f(x)=ax2+bx+c,(a<0)满足f(4)=f(1),易判断函数图象的开口方向和对称轴,然后根据自变量离对称轴距离远近与函数值大小之间的关系,即可得到答案.
解答:若二次函数f(x)=ax2+bx+c,(a<0)
且满足f(4)=f(1),
则二次函数f(x)的图象是开口朝下,以直线x= 为对称轴的抛物线
为对称轴的抛物线
∵|-1- |>|5-
|>|5- |
|
故f(-1)<f(5)
故选C
点评:本题考查的知识点是二次函数的性质,其中根据已知条件求出二次函数图象的开口方向及对称轴是解答本题的关键.
分析:根据已知中二次函数f(x)=ax2+bx+c,(a<0)满足f(4)=f(1),易判断函数图象的开口方向和对称轴,然后根据自变量离对称轴距离远近与函数值大小之间的关系,即可得到答案.
解答:若二次函数f(x)=ax2+bx+c,(a<0)
且满足f(4)=f(1),
则二次函数f(x)的图象是开口朝下,以直线x=
 为对称轴的抛物线
为对称轴的抛物线∵|-1-
 |>|5-
|>|5- |
|故f(-1)<f(5)
故选C
点评:本题考查的知识点是二次函数的性质,其中根据已知条件求出二次函数图象的开口方向及对称轴是解答本题的关键.

练习册系列答案
相关题目
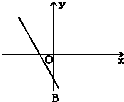 若二次函数f(x)=ax2+bx的导函数f′(x)的图象如图所示,则二次函数f(x)的顶点在( )
若二次函数f(x)=ax2+bx的导函数f′(x)的图象如图所示,则二次函数f(x)的顶点在( )| A、第四象限 | B、第三象限 | C、第二象限 | D、第一象限 |