题目内容
(本小题满分 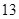 分)
分)
已知直线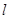 与抛物线
与抛物线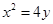 相切于点
相切于点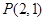 ,且与
,且与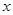 轴交于点
轴交于点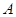 ,定点
,定点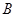 的坐标为
的坐标为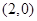 .
.
(Ⅰ)若动点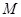 满足
满足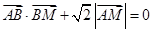 ,求点
,求点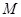 的轨迹
的轨迹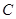 ;
;
(Ⅱ)若过点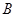 的直线
的直线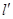 (斜率不等于零)与(I)中的轨迹
(斜率不等于零)与(I)中的轨迹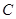 交于不同的两点
交于不同的两点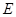 、
、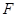 (
(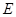 在
在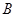 、
、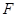 之间),试求
之间),试求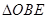 与
与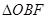 面积之比的取值范围.
面积之比的取值范围.
【答案】
解:(I)由

故 的方程为
的方程为 点A的坐标为(1,0)
…………
2分
点A的坐标为(1,0)
…………
2分
设
由
整理得: ………………
4分
………………
4分
 动点M的轨迹C为以原点为中心,焦点在x轴上,
动点M的轨迹C为以原点为中心,焦点在x轴上,
长轴长为 ,短轴长为2的椭圆.
………5分
,短轴长为2的椭圆.
………5分
(II)如图,由题意知 的斜率存在且不为零,
的斜率存在且不为零,
设 方程为
方程为 ①
①
将①代入 ,整理,得
,整理,得
 ………………7分
………………7分
设 .
. ,
,
则 ②
②
令
由此可得
由②知

 即
即  ………… 10分
………… 10分


解得
又
 面积之比的取值范围是
面积之比的取值范围是 ………… 13分
………… 13分
【解析】略

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 分)
分) 是公差不为零的等差数列
是公差不为零的等差数列 的前n项和,且
的前n项和,且 成等比数列,求数列
成等比数列,求数列 是公比不相等的两个等比数列,
是公比不相等的两个等比数列, ,证明数列
,证明数列 不是等比数列。
不是等比数列。 分)
分) )的变化情况来决定买入或卖出股票.股民老张在研究股票的走势图时,发现一只股票的
)的变化情况来决定买入或卖出股票.股民老张在研究股票的走势图时,发现一只股票的 ,则股价
,则股价 (元)和时间
(元)和时间 的关系在
的关系在 段可近似地用解析式
段可近似地用解析式 (
( )来描述,从
)来描述,从 点走到今天的
点走到今天的 点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且
点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且 对称.老张预计这只股票未来的走势如图中虚线所示,这里
对称.老张预计这只股票未来的走势如图中虚线所示,这里 段与
段与 对称,
对称, 段是股价延续
段是股价延续 .
. ,点
,点 ,点
,点 来确定解析式中的常数
来确定解析式中的常数 ,并且已经求得
,并且已经求得 .
.
 ,并回答股价什么时候见顶(即求
,并回答股价什么时候见顶(即求 股,到见顶处
股,到见顶处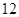 分)
分)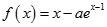 .
. 单调区间;
单调区间;  恒成立,求
恒成立,求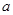 的取值范围;
的取值范围;
 分)
分) 是公差不为零的等差数列
是公差不为零的等差数列 前n项的和,且
前n项的和,且 成等比数列,求数列
成等比数列,求数列 是公比不相等的两个等比数列,
是公比不相等的两个等比数列, ,证明数列
,证明数列 不是等比数列。
不是等比数列。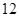 分)
分)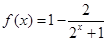 ,
,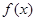 的值域。
的值域。