题目内容
在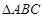 中,
中,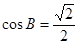 ,
,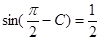 .
.
(Ⅰ)求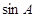 的值;
的值;
(Ⅱ)若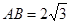 ,求
,求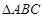 的面积.
的面积.
【答案】
(Ⅰ)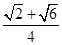 . (Ⅱ)
. (Ⅱ)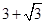 .
.
【解析】
试题分析:(Ⅰ)利用三角函数诱导公式及两角和差的三角函数.
(Ⅱ)根据正弦定理先求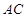 的长,利用三角形面积公式求解.
的长,利用三角形面积公式求解.
本题不难,思路比较明确,要注意认真计算.
试题解析:(Ⅰ)在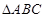 中,因为
中,因为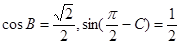 ,
,
所以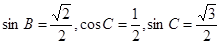 .
(3分)
.
(3分)
所以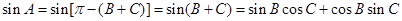
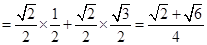 .
(6分)
.
(6分)
(Ⅱ)根据正弦定理得: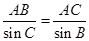 ,
,
所以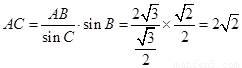 .
(9分)
.
(9分)
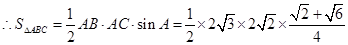
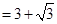 .
12(分)
.
12(分)
考点:三角函数诱导公式、两角和差的三角函数、正弦定理的应用.

练习册系列答案
相关题目
 中,
中,
 的值; (2)求
的值; (2)求 的值; (3)求
的值; (3)求 ,
, 的最小正周期;
的最小正周期; 中,已知
中,已知 为锐角,
为锐角, ,
, ,求
,求 边的长.
边的长. 为锐角,且
为锐角,且 ,函数
,函数 ,数列{
,数列{ }的首项
}的首项 .
. 的表达式;
的表达式; 中,若
中,若 A=2
A=2 ,BC=2,求
,BC=2,求 的前
的前 项和
项和