题目内容
如图,点A、B分别是椭圆![]() =1长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF.
=1长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF.

(1)求点P的坐标;
(2)设M是椭圆长轴AB上的一点,M到直线AP的距离等于|MB|,求椭圆上的点到点M的距离d的最小值.
1、P(![]() ,
,![]()
![]() ).
).
2、d最小=![]() .
.
解析:
(1)由条件A(-6,0),F(4,0).
设P(x,y).
∴![]() =(x+6,y),
=(x+6,y),![]() =(x-4,y).
=(x-4,y).
∵![]() ⊥
⊥![]() ,
,
∴0=(x+6)(x-4)+y2,即x2+2x-24+y2=0. ①
结合![]() +
+![]() =1, ②
=1, ②
解得x=![]() 或-6,代入①解得y=±
或-6,代入①解得y=±![]()
![]() 或0.
或0.
∴P(![]() ,±
,±![]()
![]() ).
).
又点P在z轴上方,∴所求P(![]() ,
,![]()
![]() ).
).
(2)由两点式得直线AP:x-![]() y+6=0.
y+6=0.
(不妨取x轴上方的P点)
设M(m,0),|MB|=6-m.
由题意6-m=![]() ,解得m=2或18(舍去).
,解得m=2或18(舍去).
∴M(2,0).
设椭圆上任一点P(x,y),
d2=MP2=(x-2)2+y2=(x-2)2+20-![]() x2
x2
=![]() x2-4x+24=
x2-4x+24=![]() (x-
(x-![]() )2+15.
)2+15.
∵-6≤x≤6,取x=![]() 得
得
d最小2=15.此时d最小=![]() .
.

练习册系列答案
相关题目
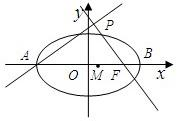 如图,点A,B分别是椭圆
如图,点A,B分别是椭圆 如图,点A、B分别是椭圆长轴的左、右端点,点F是椭圆的右焦点,其中A(-6,0),F(4,0),点P在椭圆上且位于x轴上方,
如图,点A、B分别是椭圆长轴的左、右端点,点F是椭圆的右焦点,其中A(-6,0),F(4,0),点P在椭圆上且位于x轴上方, 如图,点A、B分别是椭圆
如图,点A、B分别是椭圆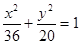 长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于
长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于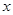 轴上方,
轴上方,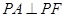 .
.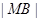 ,求椭圆上的点到点M的距离
,求椭圆上的点到点M的距离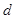 的最小值.
的最小值.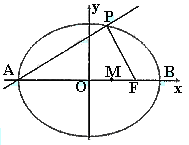
 的长轴的左右端点,点F为椭圆的右焦点,直线PF的方程为:
的长轴的左右端点,点F为椭圆的右焦点,直线PF的方程为: 且
且 。
。
 ,求椭圆上的点到
,求椭圆上的点到