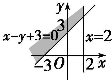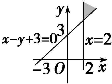Question

已知实数x，y满足不等式组

y≤x x+2y≤4 y≥ 1 2 x+m

且z=x²+y²+2x-2y+2的最小值为2．则实数m的取值范围为（　　）

A．（-∞，0）

B．（-∞，0]

C．（-∞， 4 3 ]

D．（0， 4 3 ]

Answer 1

先根据约束条件画出可行域，
其中目标函数：z=x²+y²+2x-2y+2=（x+1）²+（y-1）²，
表示可行域内点P（x，y）到（-1，1）距离的平方，如图，
因点P到直线y=x的距离即为

2

，即z=x²+y²+2x-2y+2的取值为2，
观察图形可知，当直线y=

1

2

x+m在y轴上的截距小于等于0时，此时z=x²+y²+2x-2y+2的最小值为2．即m≤0．
故选B．