题目内容

定义在R上函数f（x）满足条件：f（x+2）=数学公式，当x∈（0，2）时，数学公式，则f（2011）=________．

2
分析：函数解析式只知道一部分，而要求的函数值的自变量不在此区间上，由题设条件知本题中所给的函数是一个周期性函数，
故可以利用周期性这一性质将要求的函数值转化到区间（0，2）上求解．
解答：由题意定义在R上的函数f（x），f（2+x）=，由此式恒成立可得，此函数的周期是4．
又当x∈（0，2）时，f（x）=，则f（1）=，
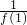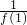由此f（2011）=f（4×502+3）=f（3）==2．
故答案为 2．
点评：本题考点是函数的值，本题考查利用函数的性质通过转化来求函数的值，是函数性质综合运用的一道好题．
对于本题中恒等式的意义要好好挖掘，做题时要尽可能的从这样的等式中挖掘出信息．
练习册系列答案
相关题目
下列6个命题中正确命题个数是（　　）
①第一象限角是锐角；
②若cos（α+β）=-1，则sin（α+2β）+sinβ=0
③函数y=sin(
π
4
-2x)的增区间是(kπ+
3π
8
，kπ+
7π
8
)，k∈Z
④角α终边经过点（a，a），（a≠0）时，sinα+cosα=
2

⑤若y=sin（ωx）的周期为4π，则ω=
1
2

⑥若定义在R上函数f（x）满足f（x+1）=-f（x），则y=f（x）是周期函数．
定义在R上函数f（x）满足f（0）=0，f（x）+f（1-x）=1，且f(
x
5
)=
1
2
f(x)当0≤x1＜x2≤1时，f（x1）≤f（x2），则f(
1
2011
)=（　　）
已知定义在R上函数f（x）部分自变量与函数值对应关系如表，若f（x）为偶函数，且在[0，+∞）上为增函数，不等式-1≤f（x）＜3的解集是（　　）
x 0 2 3 4
y -1 1 2 3
设定义在R上函数f（x）的图象与函数g（x）=a（x-2）+2（2-x）3（a为常数）的图象关于直线x=1对称．
（Ⅰ）求f（x）的解析式；?
（Ⅱ）设F(x)=(
f(x)x
+4lnx)′，当m＞0时，判断F（m3）与F（m2）的大小关系，并说明理由．
已知定义在R上函数f（x）是偶函数，对x∈R都有f（2+x）=-f（2-x），当f（-3）=-2 时，f （2007）的值为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网