题目内容
类比平面向量和空间向量,列出它们相似(相同)的性质.思路:从平面向量和空间向量的定义、运算法则、运算律、数量积、共线,共面以及向量基本定理等几个方面来进行类比.
探究:(1)从定义的角度考虑:
平面向量:平面内既有大小又有方向的向量;空间向量:空间内既有大小又有方向的向量.
(2)从运算法则的角度考虑:
两个平面向量相加的三角形法则和平行四边形法则在空间中仍成立.始点相同的三个不共面的向量之和,等于以这三个向量为棱的平行六面体的以公共始点为始点的对角线所表示的向量,这是平面向量加法的平行四边形法则在空间的推广.
(3)从运算律、数量积的角度考虑,平面向量和空间向量是相同的.
运算律:
①a+b=b+a(加法交换律);
②(a+b)+c=a+(b+c)(加法结合律);
③λ(a+b)=λa+λb(数乘分配律).
数量积的性质:
①a·e=|a|cos〈a,e〉(e是单位向量);
②a⊥b![]() a·b=0;
a·b=0;
③|a|2=a·a.
数量积的运算律:
①(λa)·b=λ(a·b);
②a·b=b·a(交换律);
③a·(b+c)=a·b+a·c(分配律).
(4)从向量共线,共面的角度考虑:
共线向量定理:向量b与a(a≠0)共线的充要条件是:有且只有一个实数λ,使得b=λa.
共面向量定理:如果两个向量a、b不共线,则向量p与向量a、b共面的充要条件是存在实数对x,y,使p=xa+yb.
(5)从向量基本定理的角度考虑:
平面向量基本定理:如果e1,e2是同一平面内的两个不共线的向量,那么对于这一平面内任一向量a,有且只有一对实数λ1,λ2,使得a=λ1e1+λ2e2,其中e1,e2表示平面向量的一组基底.
空间向量基本定理:如果三个向量a、b、c不共面,那么对于空间任一向量p,存在一个唯一的有序实数组x,y,z,使p=xa+yb+zc,其中{a,b,c}叫做空间的一个基底,a、b、c都叫基向量.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案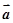 是已知的平面向量且
是已知的平面向量且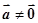 ,关于向量
,关于向量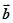 ,总存在向量
,总存在向量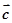 ,使
,使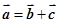 ;
;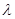 和
和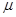 ,使
,使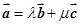 ;
;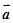 是已知的平面向量且
是已知的平面向量且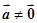 ,关于向量
,关于向量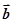 ,总存在向量
,总存在向量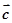 ,使
,使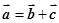 ;
;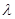 和
和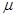 ,使
,使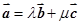 ;
;