Question

平面上点P与点F(0，1)的距离比它到直线y+2=0的距离小1．

(Ⅰ)求出点P的轨迹方程；

(Ⅱ)过点F作点P的轨迹的动弦CD，过C、D两点分别作点P的轨迹的切线，设其交点为M，求点M的轨迹方程，并求出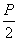的值．

 

Answer 1

解:(Ⅰ)由已知条件，点P与点F距离等于它到直线y=-1的距离，故其轨迹为以F(0，1)为焦点的抛物线．

∵=1  ∴P=2  故点P的轨迹方程为x²=4y

(Ⅱ)设C(x₃，)，D(x₄，)

过抛物线上C、D两点的切线方程分别是

y=

∴两条切线的交点M的坐标为()

设CD的直线方程为y=nx+1，代入x²=4y得x²-4nx-4=0

∴x₃x₄=-4  故M的坐标为(，-1)

故点M的轨迹为y=-1

∵=(x₃，-1)    =(x₄，-1)

∴·=x₃x₄+

=x₃x₄+1-

而=+(-1-1)²

=+4=

故=-1