题目内容
(本小题满分12分)
已知一种名贵花卉种子的发芽率为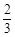 ,现种植这种种子4粒,求:
,现种植这种种子4粒,求:
(Ⅰ)至少有3粒发芽的概率;
(Ⅱ)种子发芽的粒数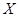 的分布列及平均数.
的分布列及平均数.
已知一种名贵花卉种子的发芽率为
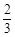 ,现种植这种种子4粒,求:
,现种植这种种子4粒,求:(Ⅰ)至少有3粒发芽的概率;
(Ⅱ)种子发芽的粒数
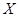 的分布列及平均数.
的分布列及平均数. (Ⅰ) ;
;
(Ⅱ) 的分布列如下:
的分布列如下:
 ,
, .
.
 ;
;(Ⅱ)
 的分布列如下:
的分布列如下: | 0 | 1 | 2 | 3 | 4 |
| P |  |  |  |  |  |
 ,
, .
. 本试题主要是考查了随机变量的分布列的球结合哦数学期望值的运用。
(1)一种名贵花卉种子的发芽率为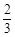 ,现种植这种种子4粒,可以看做4此独立重复试验,则利用概率公式解得
,现种植这种种子4粒,可以看做4此独立重复试验,则利用概率公式解得
2)因为种子发芽的粒数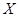 服从二项分布,因此可知分布列和期望值。
服从二项分布,因此可知分布列和期望值。
解析:(Ⅰ)设“至少有3粒种子发芽”为事件A,则
 ,
,
故所求概率为 6分(Ⅱ)
6分(Ⅱ) 的分布列如下:
的分布列如下:
10分
 ,
, . 12分
. 12分
(1)一种名贵花卉种子的发芽率为
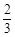 ,现种植这种种子4粒,可以看做4此独立重复试验,则利用概率公式解得
,现种植这种种子4粒,可以看做4此独立重复试验,则利用概率公式解得2)因为种子发芽的粒数
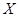 服从二项分布,因此可知分布列和期望值。
服从二项分布,因此可知分布列和期望值。解析:(Ⅰ)设“至少有3粒种子发芽”为事件A,则
 ,
, 故所求概率为
 6分(Ⅱ)
6分(Ⅱ) 的分布列如下:
的分布列如下: | 0 | 1 | 2 | 3 | 4 |
| P |  |  |  |  |  |
 ,
, . 12分
. 12分
练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
 为选出的4个人中选科目甲的人数,求
为选出的4个人中选科目甲的人数,求 是一个离散型随机变量,其分布列如下表,试求随机变量
是一个离散型随机变量,其分布列如下表,试求随机变量 与方差
与方差 .
.
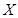 为选出的4名选手中女选手的人数,求
为选出的4名选手中女选手的人数,求 的值.
的值. ,求
,求 ,三人都做对的概率是
,三人都做对的概率是 ,三人全做错的概率是
,三人全做错的概率是 ,已知乙做对这道题的概率大于丙做对这道题的概率.设三人中做对这道题的人数为
,已知乙做对这道题的概率大于丙做对这道题的概率.设三人中做对这道题的人数为 ,则随机变量
,则随机变量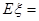 .
.