题目内容
已知函数f(x)=2a·4x-2x-1.
(1)当a=1时,求函数f(x)的零点;
(2)若f(x)有零点,求a的取值范围.
解:(1)当a=1时,f(x)=2·4x-2x-1.
令f(x)=0,即2·(2x)2-2x-1=0,解得2x=1或2x=-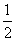 (舍去).
(舍去).
∴x=0,∴函数f(x)的零点为x=0. --------------------------4
(2)解法一:若f(x)有零点,则方程2a·4x-2x-1=0有解----------------6
于是2a=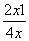
=(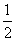 )x+(
)x+(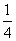 )x ----------------------------------------------------------10
)x ----------------------------------------------------------10
∵(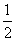 )x>0,∴2a>
)x>0,∴2a>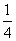 -
-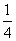 =0,即 a>0.------------------------------12
=0,即 a>0.------------------------------12
解法二:令t=2x,∵x∈R,∴t>0,
则方程2at2-t-1=0在(0,+∞)上有解. ------------------------6
①当a=0时,方程为t+1=0,即t=-1<0,
此时方程在(0,+∞)无解.-----------------------------------------8
②当a≠0时,令g(t)=2at2-t-1,
若方程g(t)=0在(0,+∞)上有一解,则ag(0)<0,即-a<0,解得a>0.
若方程g(t)=0在(0,+∞)上有两解,则
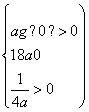 无解
无解
-------------------------------------------10
综上所述,所求实数a的范围是(0,+∞). --------------------------12

 阅读快车系列答案
阅读快车系列答案 的最大值是 .
的最大值是 .  ,若
,若 ,则
,则 ,
, 大小关系是( )
大小关系是( )


 ,b=
,b= ,c=
,c= 0.3,则a,b,c三个数的大小关系是________
0.3,则a,b,c三个数的大小关系是________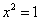 ,则
,则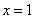 ”的否命题为:“若
”的否命题为:“若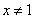 ”.
”.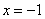 ” 是“
” 是“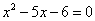 ”的必要不充分条件.
”的必要不充分条件.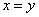 ,则
,则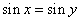 ”的逆否命题为真命题.
”的逆否命题为真命题.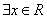 使得
使得 ”的否定是:“
”的否定是:“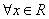 均有
均有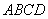 的长
的长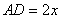 ,宽
,宽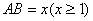 ,线段
,线段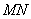 的长度为1,端点
的长度为1,端点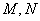 在长方形
在长方形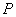 所形成的轨迹为
所形成的轨迹为 ,记
,记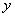 ,则函数
,则函数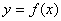 的图象大致为 ( )
的图象大致为 ( )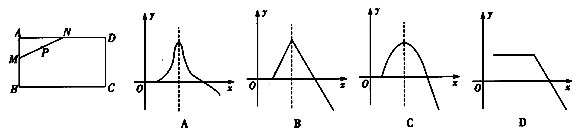
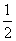 ,则他应击中靶心5次
,则他应击中靶心5次